Generating Adversarial Examples for Holding Robustness of Source Code Processing Models

Part1. title&Source

Title: Generating Adversarial Examples for Holding Robustness of Source Code Processing Models
Conference: The Thirty-Fourth AAAI Conference on Artificial Intelligence (AAAI-20)

Part2. abstract

本文提出了一种基于Metropolis-Hastings采样的标识符重命名技术，名为Metropolis-Hastings Modifier (MHM)，用于生成对源代码处理模型的对抗样本。在功能分类基准上的深度评估表明，MHM在生成源代码对抗样本方面是有效的，并且通过对抗训练能够显著增强深度学习模型的鲁棒性。

Part3. introduction

近年来，自动化源代码处理、分析与生成是软件系统生命周期中的关键活动，深度学习模型被应用于多种源代码处理任务，如功能分类、克隆检测、代码补全等。然而，现有的深度学习模型缺乏对抗鲁棒性，容易被对抗样本攻击。与图像、音频和自然语言的对抗样本不同，编程语言的结构化特性给对抗攻击带来了新的挑战。本文提出了一种新方法MHM，通过基于Metropolis-Hastings采样的标识符重命名生成对抗样本，用于攻击源代码处理的深度学习模型，并通过对抗训练来增强模型的鲁棒性。

本文贡献包括：

• 确认了用于代码处理的深度学习模型也有鲁棒性问题
• 提出一个简单且有效的算法MHM
• 设计实验证明其有效性
• 进行对抗性训练，增加了DL模型的鲁棒性

Part4. conclusion

本文确认了深度学习模型在源代码处理任务中的非鲁棒性问题，并提出了MHM算法来生成对抗样本。实验表明，MHM能够有效地生成对抗样本并攻击目标模型，同时通过对抗训练来增强模型的鲁棒性。在未来工作中，作者计划引入更复杂的语义解析与树结构修正，以进一步提高对抗攻击能力。

Part5. related work

源代码分类：

• 数据集

数据集$D$ 表示为：

$D={(x_i,y_i)}_{i=1}^N$  

其中，$x_i$ 是源代码片段，$y_i$ 是对应的标签，用one-hot向量表示。整个数据集分为训练集$D^{(t)}$ 、验

证集$D^{(v)}$ 和测试集$D^{(e)}$ 。

• 特征：

特征表示为从输入到标量的映射，记为$f:X\to R$ ,这些特征被分类模型用于判断源代码片段的类

別。

• 分类模型：

分类模型$C$ 被定义为：

$C(x)=\sigma(f_1(x),f_2(x),\ldots,f_k(x))$

其中，$\sigma$ 是softmax分类函数。模型通过在训练集上的损失最小化进行训练：

$J(D^{(t)}|C)=-\frac1{N^{(t)}}\sum_{i=1}^{N^{(t)}}\sum y_i\circ\log C(x_i)$ 通过最小化损失函数，模型能够在测试集上获得良好的性能，但仍然容易受到对抗攻击。

∘表示点乘

对抗性攻击

包括3种算法：

• 最大化优化问题

$\begin{aligned}\max_{\hat{x}}&\sum y\circ\log\frac1{C(x)},\&\mathrm{s.t.}\hat{x}\in\mathcal{E}\wedge~\forall i\in\mathcal{I},E(i|\hat{x})=E(i|x)\quad\text{(5)}\end{aligned}$

• 梯度上升以生成对抗性示例，这些方法以非常有限的迭代来扰乱基于梯度信息的示例，一次迭代示例：

$x_{t+1}=x_t+\alpha\cdot\operatorname{sign}(\nabla_x\sum y\circ\log\frac1{C(x)})\quad\text{(6)}$

• 采样问题处理，例如GeneticAttack 通过遗传算法执行采样

$\pi(x)\propto(1-\mathcal{C}(x)[y])\cdot\mathcal{X}_1\cdots\mathcal{X}_k\quad\quad(7)$

其中 C(x)[y] 是 C 预测的类 y 的概率，而 X1 · · ·， Xk 是词汇、语法和句法约束的指示函数

作者采用基于采样的方法，对对抗性攻击进行 M-H 采样。因为由于代码是离散的，基于优化和基于梯度的方法难以实现

对抗性训练

• 首先用$\mathcal{D}{(t)}$生成对抗性数据集$\mathcal{D}_{adv}^{(t)}.$

• 然后用$\mathcal{D}_{adv}^{(t)}.$从头开始训练同目标模型具有相同架构和超参数的模型

健壮性

Useful feature：

ρ 有用的特征与分类标签密切相关。在二元分类中，有用的特征定义为：

$E_{(x,y)\sim\mathcal{D}}[y\cdot f(x)]\geq\rho\quad\quad\quad\quad\quad(8)$

其中 ρ > 0。ρ 度量特征 f (x) 和分类标签 y 之间的相关性。ρ 越大，相关性越强。

Robust feature：

γ-robust features 是有用的特征且任何允许的扰动之后仍然有用。如果分类器对稳健特征进行预测，它就会获得对对抗性攻击的抵抗能力。在二元分类中，robust features定义为

$E_{(x,y)\sim\mathcal{D}}[\inf_{x’\in\Delta(x)}y\cdot f(x’)]\geq\gamma\quad\quad(9)$

其中 Δ(x) 是完整的扰动 x 集合，满足编程语言的词汇、语法和句法约束的所有元素

Non-Robust feature：

Non-Robust feature也是有用的特征，但对于任何γ > 0 来说都不是γ稳健的。对抗性攻击主要扰动非鲁棒特征，因为对 x 的任何扰动都可能导致非鲁棒 f (x) 发生巨大变化。

Part6. model&algorithm

MHM算法被设计用于生成源代码的对抗样本，通过对目标模型(如LSTM、ASTNN)进行攻击。MHM算法的基本思想是通过Metropolis-Hastings采样，迭代地对标识符进行重命名。

MHM 以受到攻击的源代码分类器 (C) 和一对正确分类的数据 ((x， y) ∈ D)作为输入，并输出一系列对抗性样本(xˆ1， xˆ2， · · · )。

对抗性样本应该满足三个要求：

• 能够误导选择的模型
• 没有编译错误且能正常运行
• 输出结果同正常示例一样

M-H 算法是一种经典的马尔可夫链蒙特卡洛采样方法，给定一个平稳分布π(x)和转换提议，M-H能够生成理想的样本，在每次迭代中，M-H都会根据转换分布 (Q(x′|x)) 提出的建议从 x 跳转到 x’。 接受后，算法跳转到 x′ 并对 x′ 进行采样。否则，它将保持在 x 处，不执行采样。

$\alpha(x^{\prime}|x)=\min{1,\alpha^{*}}=\min{1,\frac{\pi(x^{\prime})Q(x|x^{\prime})}{\pi(x)Q(x^{\prime}|x)}}\quad(10)$

参考M-Hsamping，在每次迭代中MHM包括3个步骤：

1. 选择源标识符：从源代码中选取可以重命名的标识符。
2. 选择目标标识符：从词汇集中选择新的标识符来替换源标识符。
3. 接受或拒绝提案：基于Metropolis-Hastings采样的接受率决定是否接受重命名提案。

阶段 1 和 2 生成过渡提案，阶段 3 接受或拒绝提案，接受率给出概率。由于标识符重命名的操作是可逆的，因此 MHM 中的过渡是非周期性的和遍历的，使 MHM 最终收敛。算法的单次迭代逻辑：

transition proposal 过渡提案

• 在源代码中收集所有的变量和函数的声明和定义形成集合S(x)，然后以相等的概率从集合中抽取源标识符(5-6行)
• 候选标识符集 (T(x)) 由整个词汇集(V)生成,T(x)中的元素必须满足之前提到的标识符的词法规则，并且不能出现在 S(x) 中，确保重命名后的代码仍然满足公式4，目标标识符 (t) 以相等的概率从 T (x) 中提取(7-8行)
• 过渡建议将 x 中的 s 重命名为 t，形成 x′。转移概率定义为

$\begin{aligned}Q(x’|x)&\propto\mathcal{I}{s\in\mathcal{S}(x)\wedge t\in\mathcal{T}(x)}\cdot P_{\mathcal{S}(x)}(s)\cdot P_{\mathcal{T}(x)}(t),\&\mathrm{where~}\mathcal{S}(x)\cap\mathcal{T}(x)=\emptyset\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(11)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{aligned}$

· $Q( x^{\prime }| x)$ :表示从代码片段$x$ 到$x^{\prime}$ 的转移概率。

·$I{s\in S(x)\land t\in T(x)}$ :指示函数，确保源标识符$s$ 必须在代码片段$x$ 中的可重命名

标识符集合$S(x)$ 中，目标标识符$t$ 必须在候选标识符集合$T(x)$ 中。

,$P_{S(x)}(s)$ :从集合$S(x)$ 中选取源标识符$s$ 的均匀概率。·$P_{T(x)}(t)$ :从集合$T(x)$中选取目标标识符$t$ 的均匀概率。

$P_{\mathcal{S}(x)}(s)和 P_{\mathcal{T}(x)}(t)$ 分别是从S(x)和T(x)中绘制的均匀分布并且S(x)和T(x)不相交

Acceptance Rate

在第 1 阶段和第 2 阶段提出的过渡提案被接受，其接受率由第 3 阶段给出，接受率 （α） 是根据转换概率和倒置转换概率计算的。如果接受过渡提案，则 x 中的 s 将重命名为 t，反之重命名后的源码片段将 C测试，以验证它是否为对抗性示例(9-22)

$\alpha^*(x’|x)=\frac{\pi(x’)Q(x|x’)}{\pi(x)Q(x’|x)}=\frac{(1-C(x’)[y])\cdot P_{S(x’)}(t)\cdot P_{T(x’)}(s)}{(1-C(x)[y])\cdot P_{S(x)}(s)\cdot P_{T(x)}(t)}\approx\frac{1-C(x’)[y]}{1-C(x)[y]})(12)$

$\alpha^*(x^{\prime}|x)$ :表示从代码片段$x$ 转移到代码片段$x^\prime$ 的未归一化接受率。

$\pi(x)$ :目标分布，表示代码片段$x$ 的对抗性程度，越容易误导模型的代码片段，其目标分

布值越高。

$Q(x^{\prime}|x)$ :从代码片段$x$ 转移到代码片段$x^{\prime}$ 的转移概率。

$C(x)[y]$ :表示分类模型$C$ 对输入代码片段$x$ 预测为正确标签$y$ 的概率。

$P_{S(x)}(s)$ 和$P_{T(x)}(t)$ :均匀分布，从集合$S(x)$ 和$T(x)$ 中选择标识符的概率。

结果大于1表示100%接受

Part7. experiment

实验设置

• 数据集：实验选择了Open Judge (OJ) 数据集，该数据集包含52,000个C/C++代码文件，分属于104个功能类别。
• 目标模型：采用LSTM和ASTNN作为攻击目标模型，其中LSTM适用于序列处理，ASTNN是当前在OJ数据集上性能最好的模型。

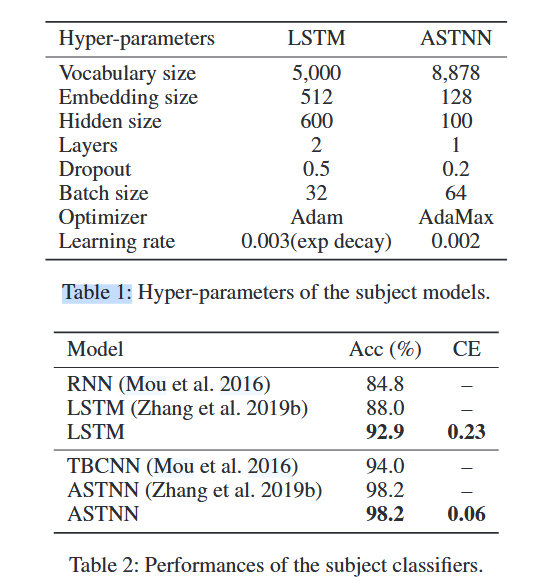
• 基线算法：实验中将GeneticAttack (GA) 算法作为基线.它维护了一个序列群，并根据黑盒设置下的嵌入距离（独立于模型检索）通过word-level替换进行扰动。然后，通过分类器和语言模型过滤中间句子，从而引向下一代

对抗攻击实验

实验选取了1,000个样本，对LSTM和ASTNN进行攻击。结果表明，MHM对LSTM和ASTNN的攻击成功率分别为71.3%和92.1%，并且所有生成的对抗样本均有效(符合词法和语法规则)。相比之下，基于GeneticAttack的攻击生成的大多数样本由于无法通过编译而无效。

实验采用Attack Rate、validity rate和Final Success Rate作为评估

对抗训练实验

通过使用MHM生成的2,000个对抗样本进行对抗训练，结果显示经过对抗训练的模型对MHM的攻击有更强的抵抗能力。LSTM模型的准确率从92.9%提升到94.0%，对抗成功率下降至46.4%。ASTNN模型在对抗训练后攻击成功率也从92.1%下降至54.7%。

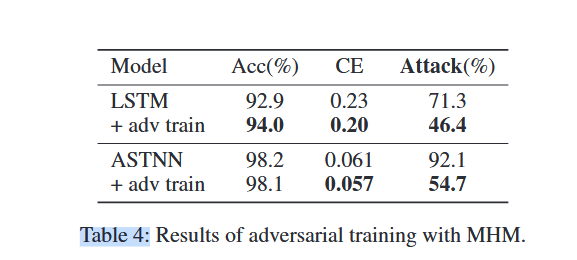
同时，对抗性样本数量对模型性能也有影响，结果表明，数量有一个阈值，在阈值之前随着数量增长，模型鲁棒性会提升。达到阈值后，随着对抗性样本数量的增加，对抗性训练的模型往往会失去性能

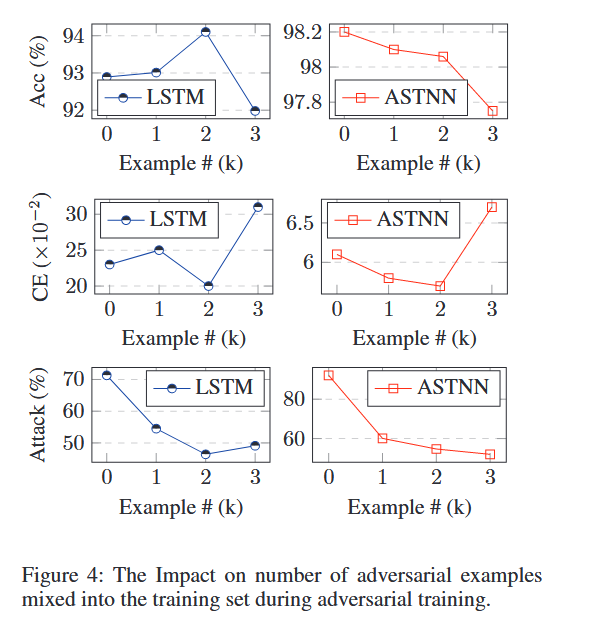
标识符名称是有用非鲁棒性特征，对抗训练的目的是提高模型对对抗样本的抵抗力，使其不再依赖非鲁棒特征

Part8. discussion&future work

实验结果表明，标识符是源代码处理模型中的非鲁棒特征，对标识符的修改能够有效地攻击模型。因此，通过对抗训练能够减少模型对这些非鲁棒特征的依赖，增强其鲁棒性。在未来的工作中，作者计划引入更多基于语义解析的树结构修正，例如将“for”语句转换为“while”语句，以生成更多样化的对抗样本。