算法

无标签
面试相关
发布日期:   2024-08-06
文章字数:   16.2k
阅读时长:   78 分
阅读次数:  

算法

动态规划

股票问题

一次买卖

image-20230920123959039

算法思想：

​ 因为只有一次买卖，不需要存储之前的状态，与动态规划关系不大。

​ 考虑到顺序，定义一个minprice初始化为最大值，进行一次遍历，maxprofit初始化为0

​ 进行判断，更新最小值已经最大利润

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int inf = 1e9;
        int minPrice = inf;
        int maxprofit = 0;
        int n = prices.size();
        for(int i = 0; i < n; i++){
            minPrice = min(prices[i] , minPrice);
            maxprofit = max(maxprofit, prices[i] - minPrice);
        }
        return maxprofit;
    }
};

无限交易，最多持有一股

image-20230920124506291

思路：

​ 基本的动态规划问题。dp[i] [0]:第i天不持有股票的最大利润。dp[i] [1]:第i天持有股票的最大利润。

​ 状态转移方程：持有股票：可能是之前持有，也可能是今天买入，所以两种方式取最大值

​ 不持有股票：同理，可能是之前就不持有，也可能是今天卖出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        int dp[n][2];
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for(int i = 1; i < n; i++){
            dp[i][0] = max(dp[i  -1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
        }
        return dp[n - 1][0];
    }
};

两笔交易，最多持有一股

image-20230920125417152

思路:

​ 因为只能有两次，所以用dp[n] [4] 来记录四个状态，大致思路跟上题一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int n = prices.size();
        if(n < 2){
            return 0;
        }
        vector<vector<int>> dp(n, vector<int>(5)); // 创建一个二维动态规划数组dp，其中dp[i][j]表示在第i天结束时，处于状态j时的最大利润
        dp[0][0] = 0; // 第一天不持有股票，利润为0
        dp[0][1] = -prices[0]; // 第一天持有股票，利润为-price[0]（购买股票的成本）
        dp[0][3] = -prices[0]; // 第一天持有股票且已进行过一次交易，利润为-price[0]

        for(int i = 1; i < n; i++){
            dp[i][1] = max(dp[i-1][1], -prices[i]); // 在第i天持有股票，可以是前一天就持有或者今天购买的最大利润
            dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i]); // 在第i天卖出股票，可以是前一天就卖出或者今天卖出的最大利润
            dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i]); // 在第i天持有股票且已进行过一次交易，可以是前一天就持有或者今天购买的最大利润
            dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i]); // 在第i天卖出股票且已进行过两次交易，可以是前一天就卖出或者今天卖出的最大利润
        }
        return dp[n - 1][4]; // 返回最终最大利润，即在第n天结束时且已经进行了两次交易的状态下

k次交易，最多持有一股

image-20230920131206587

思路：

​ 与上一题基本相似，不同之处在于你需要将次数抽象成2 * k + 1；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        if(n < 2 || k == 0){
            return 0;
        }
        vector<vector<int>> dp(n,vector<int>(2 * k + 1));
        dp[0][0] = 0;
        int tmp = 1;
        while(tmp <= 2 * k){
            dp[0][tmp] = -prices[0]; 
            tmp += 2;
        }

        for(int i = 1; i < n; i++){
            for(int j = 1; j <= 2 * k; j += 2){
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i]);
            }
            for(int j = 2; j <= 2 * k; j += 2){
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + prices[i]);
            }
        }
        
        int max_profit = 0;
        for(int i = 0; i <= 2 * k; i += 2){
            max_profit = max(max_profit, dp[n - 1][i]);
        }
        
        return max_profit;
    }
};

打家劫舍问题

非循环遍历

image-20230922130832380

算法思想：

制约条件只有一个：不能连着计算。很容易就确定了状态转移方程

​ dp[i] = max(dp[i - 1], dp[i - 2] + nums[i];

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int rob(vector<int>& nums) {
        // dp[i]: 到第i家的最高金额
        int n = nums.size();
        int dp[n + 1];
        dp[0] = 0;
        dp[1] = nums[0];
        for(int i = 2; i <= n; i++){
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1]);
        }
        return dp[n];
    }
};

循环问题

image-20230923150327595

思路：因为有还，所以必须考虑首尾问题。即第一户和最后一户不能同时偷。

​ 所以把这个问题拆解成两个子问题即可解决：即考虑第一户到第n - 1户 和 考虑第二户到第n户

​ 这样变成两个非循环问题，将实现逻辑封装起来就可以解决

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
private:
    vector<int> dp;
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n == 0){
            return 0;
        }
        if(n == 1){
            return nums[0];
        }
        // dp[i] : 第i户能偷到的最大金额
        
        /*
            将这题的思路分解成两种情况，考虑第一间房或者考虑最后一间房
            因为这两间房是连在一起的，不能同时偷窃
        */
        int planA = robRange(nums, 0, n - 2);
        int planB = robRange(nums, 1, n - 1);
        return planA > planB ? planA : planB;
    }
    int robRange(vector<int>& nums,int l, int r){
        if(l == r){
            return nums[l];
        }  
        dp.resize(nums.size(), 0);
        dp[l] = nums[l];
        dp[l + 1] = max(nums[l], nums[l + 1]);
        for(int i = l + 2; i <= r; i++){
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[r];
    }
};

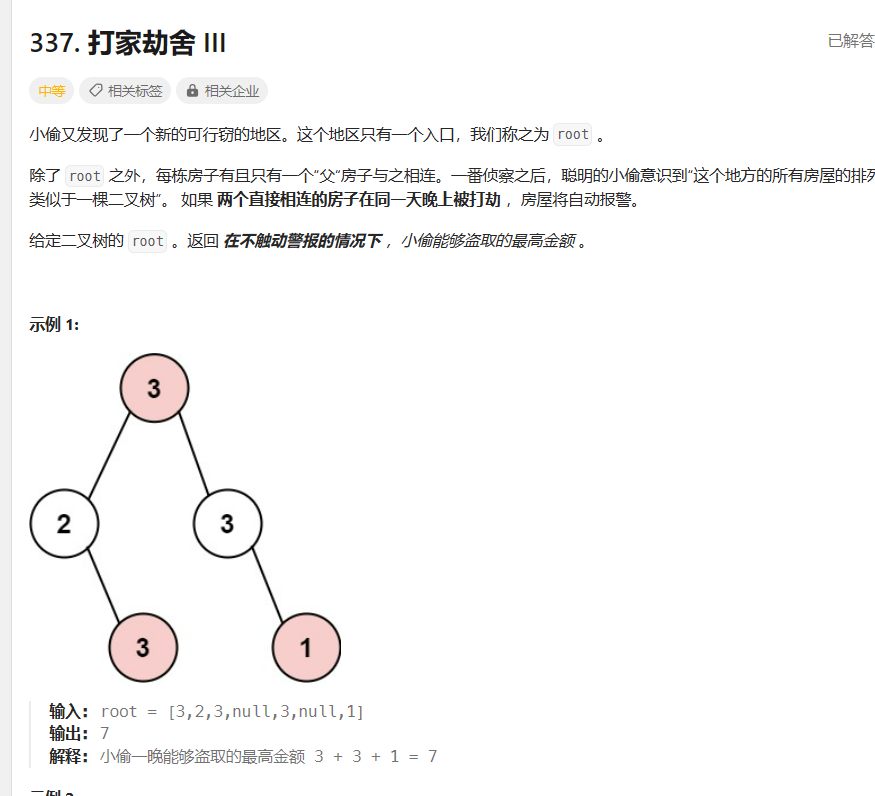
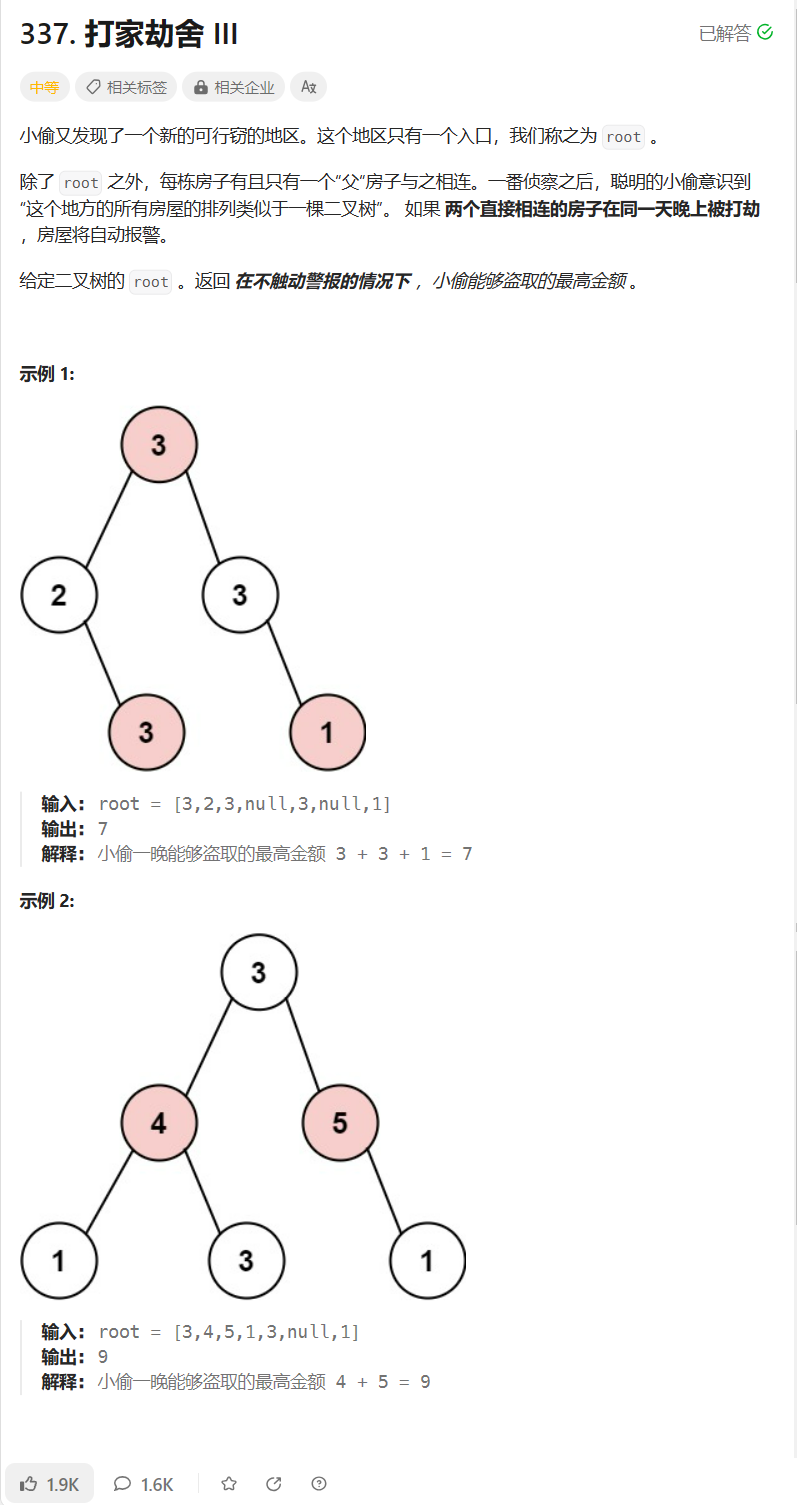
二叉树形(树桩dp)

image-20230923150403188

此题是树状dp的入门题

根据题意：偷了父节点，两个子节点遍不能再投。所以每一层可以用dp[2]来表示。dp[0]表示不偷该层的最大值，dp[1]表示偷了该层的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> ret = treerob(root);
        return max(ret[0], ret[1]);
    }
    vector<int> treerob(TreeNode* root){
        if(root == nullptr){
            return {0, 0};
        }
        vector<int> dp(2);
        auto l = treerob(root->left);
        auto r = treerob(root->right);
        dp[0] = max(l[0], l[1]) +  max(r[0], r[1]);
        dp[1] = l[0] + r[0] + root->val;
        return dp;
    }
};

最长公共子序列

image-20230920224238172

思路：

​ 确定状态转移方程：if(text1[i - 1] == text2[j - 1]){

​ dp[i] [j] = dp[i - 1] [j -1] + 1;

​ }else{

​ dp[i] [j] = max(dp[i - 1] [j], max(dp[i] [j - 1], dp[i - 1] [ j - 1]));

​ }

dp[i] [j] :表示前一个字符串的0-i位和后一个字符串的0-j位中最长的公共前缀

当t1[i] == t2[j] 时，该长度为之前长度+ 1

不相等时，另外三种情况取最大值(写的比较简略，详见代码逻辑)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n1 = text1.size();
        int n2 = text2.size();
        int dp[n1 + 1][n2 + 1];
        for(int i = 0; i <= n1; i++){
            dp[i][0] = 0;
        }
        for(int j = 0; j <= n2; j++){
            dp[0][j] = 0;
        }
        for(int i = 1; i <= n1; i++){
            for(int j = 1; j <= n2; j++){
                if(text1[i - 1] == text2[j - 1]){
                    dp[i][j] = dp[i - 1][j  -1] + 1;
                }else{
                    dp[i][j] = max(dp[i - 1][j], max(dp[i][j - 1], dp[i - 1][ j - 1]));
                }
            }
        }
        return dp[n1][n2];
    }
};

接雨水

image-20230922101855341

对于下标i，水能达到的最大高度等于下标i的最大高度的最小值，下标i处能接的雨水量等于下标i处水能到达的最大高度减去height[i]

动态规划：

创建两个长度为n的数组leftMax和rightMax，分别表示i及其左边和及其右边的最大值。

我的思路：分别算出左右的最高高度，然后算出每一列能得到的最大雨水量相加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        int leftMax[n];
        int rightMax[n];
        leftMax[0] = height[0];
        rightMax[n - 1] = height[n - 1];
        int ret = 0;
        for(int i = 1; i < n; i++){
            leftMax[i] = max(leftMax[i - 1], height[i]);
        }
        for(int i = n - 2; i >= 0; i--){
            rightMax[i] = max(rightMax[i + 1], height[i]);
        }
        for(int i = 0; i < n; i++){
            int h = min(leftMax[i], rightMax[i]);
            ret += h - height[i];
        }
        return ret;
    }
};

目标和

image-20230922124129143

这道题可以用dfs解决，现在主要巩固练习动态规划

算法思路：

​ 加法总和为x，减法总和就是sum - x

​ 希望得到 x - (sum - x) = target

​ x = (sum + target) / 2

因此可以将该题抽象为装满容量为x的背包有多少种方法

​ 注意：当 x 为奇数时，代表没有方法，直接返回0

状态转移方程：

​ 若不计算该点：dp[i] [j] = d[i - 1] [j] ，

​ 若计算该点：注意此时需要相加，因为最后算的是有多少种情况 dp[i] [j] += dp[i - 1] [j - nums[j] ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(auto& n : nums){
            sum += n;
        }
        if(sum < target || (sum - target) % 2 != 0){
            return 0;
        }
        int x = (sum - target) /2;
        int n = nums.size();
        // dp[i][j]: 到第i个数字时和为j的数量
        vector<vector<int>> dp(n + 1,vector<int>(x + 1));
        dp[0][0] = 1;
        for(int i = 1; i <= n; i++){
            int num  = nums[ i - 1];
            for(int j = 0; j <= x; j++){
                dp[i][j] = dp[i - 1][j]; // 不选择当前数字
                if(j >= num){
                    dp[i][j] += dp[i - 1][j - num]; // 选择当前数字
                }
            }
        }
        return dp[n][x];
    }
};

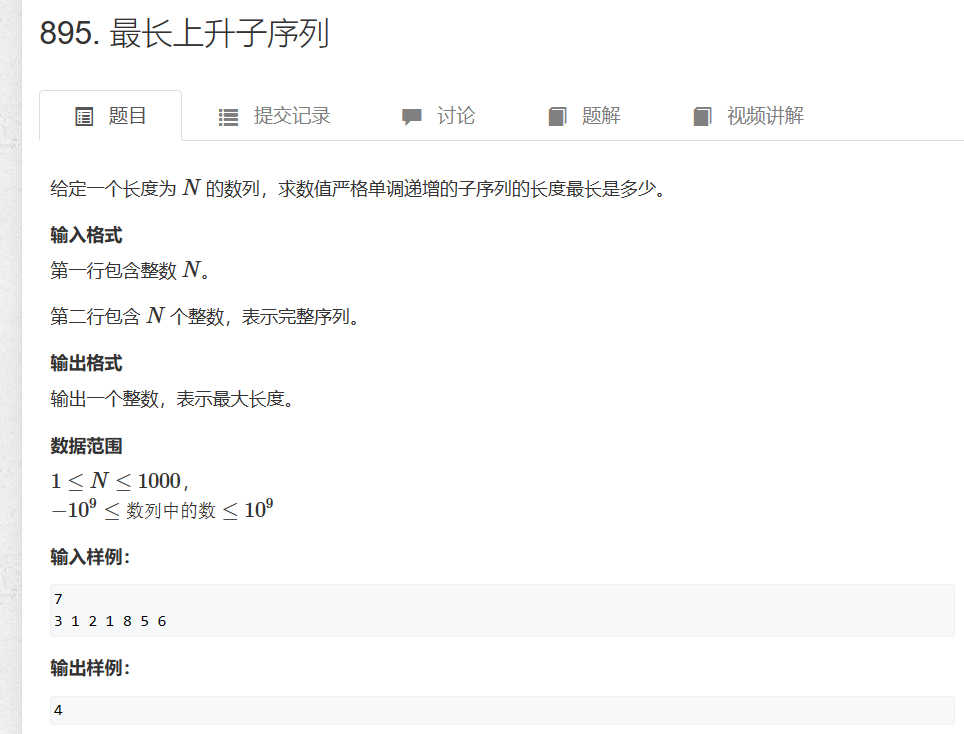
最长上升子序列

image-20231005154611505

思路：

​ dp[i]表示以i结尾的元素的最长子序列的长度。

​ 如何计算：即 dp0 , 1, 2 … i - 1的长度的最大值 + 1

​ 所以两层for循环，时间复杂度为O(N²)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <vector>
#include <climits>

using namespace std;

const int N = 1010;
int n;
vector<int> dp;
int nums[N];

int max_length(){
    dp[0] = 1;
    for(int i = 1; i < n; i++){
        dp[i] = 1;
        for(int j = 0; j < i; j++){
            if(nums[i] > nums[j]){
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
    }
    int ret = dp[0];
    for(int i = 1; i < n; i++){
        if(dp[i] > ret){
            ret = dp[i];
        }
    }
    return ret;
}

int main(){
    scanf("%d\n", &n);
    dp.resize(n);
    for(int i = 0; i < n; i++){
        scanf("%d", &nums[i]);
    }
    int ret = max_length();
    printf("%d", ret);
    return 0;
}
  • 优化

时间复杂度O(N²)的算法容易超时

  • 观察发现，当最大长度相同的数值中，只需要存数值最小的那一个即可，因为满足大的数组一定满足小的数值(递增子序列)
  • 随着长度的增加，结尾值的大小一定是严格递增的
  • 求以a[i]结尾的最长上升子序列的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <algorithm>

using namespace std;
const int N = 100010;
int n;
int a[N], q[N]; //q[i]:长度为i的元素的最大值

int main(){
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &a[i]);
    }
    q[0] = -2e9;
    int len = 0; //序列和长度
    for(int i = 0; i < n; i++){
        int l = 0, r = len;
        while(l < r){
            int mid = (l + r + 1) >> 1;
            if(q[mid] < a[i]){
                l = mid;
            }else{
                r = mid - 1;
            }
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    printf("%d\n", len);
    return 0;
}

最长公共子序列

image-20231006115808602

思路:

​ dp[i] [j]:表示text1 的前i个字符和text2的前j个字符的最长公共前缀

​ 状态转移方程有两种情况

​ 当text1[i] == text2[j]时：dp[i] [j] = dp[i - 1] [ j - 1] + 1

​ 不相等时：dp[i] [j] = max(dp[i - 1] [j - 1], max(dp[i - 1] [j], dp[i] [j - 1]))；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>
using namespace std;

const int N = 1010;
char a[N], b[N];

int longestCommonSubsequence(string text1, string text2) {
    int n1 = text1.size();
    int n2 = text2.size();
    vector<vector<int>> dp(n1 + 1,vector<int>(n2 + 1));
    for(int i = 1; i <= n1; i++){
        for(int j = 1; j <= n2; j++){
            if(text1[i - 1] == text2[j - 1]){
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }else{
                dp[i][j] = max(dp[i - 1][j - 1], max(dp[i - 1][j], dp[i][j - 1]));
            }
        }
    }
    return dp[n1][n2];
}

int main(){
    int n1, n2;
    scanf("%d%d\n", &n1, &n2);
    // char a[n1], b[n2];
    scanf("%s%s", a, b);
    string s1 = a;
    string s2 = b;
    // cout << s1 << endl;
    // cout << s2 << endl;
    int ret = longestCommonSubsequence(s1, s2);
    printf("%d\n", ret);
}

最短编辑距离（字符串类问题）

解决两个字符串的动态规划问题，一般是用两个指针ij分别指向两个字符串的最后，然后一步步往前移动，缩小规模问题(也可以从前往后移动)

image-20231006150134792

思路：

​ 状态转移方程

​ 当word1[i - 1] == word2[j - 1]：dp[i] [j] = dp[i- 1] [j - 1];

​ 当word1[i - 1] != word2[j - 1]：相当于要在插入、删除、替换操作中选取操作次数最小的.

  • A变换成b
    • 删除A：dp[i - 1] [j]
    • 增添A: 相当于删除B：dp[i] [j - 1]
    • 替换A：相当于删除A和：dp[i - 1] [j - 1]
    • 取三者最小值 + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include <iostream>
#include <vector>
using namespace std;
const int N = 1010;
int n ,m;
char a[N], b[N];

int minDistance(string word1, string word2){
    //dp[i][j]: word1的前i个字符和
    vector<vector<int>> dp(n + 1, vector<int>(m + 1));
    //
    for(int i = 0; i <= n; i++){
        dp[i][0] = i;
    }
    for(int j = 0; j <= m; j++){
        dp[0][j] = j;
    }
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            if(word1[i - 1] == word2[j - 1]){
                dp[i][j] = dp[i - 1][j - 1];
            }else{
                dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
            }
        }
    }
    return dp[n][m];
}

int main(){
    scanf("%d%s",&n,a);
    scanf("%d%s",&m,b);
    string s1(a);
    string s2(b);
    int ret = minDistance(s1,s2);
    printf("%d\n",ret);
    return 0;
}

记忆化搜索

记录运算结果，避免重复运算的方法就是记忆化搜索

  • 记忆化搜索 = 深度优先搜索的实现 + 动态规划的思想
  • 步骤：
    • 1.合法性剪枝
      • 因为在递归计算的时候，我们必须保证传入参数的合法性，所以这一步是必要的，比如坐标为负数之类的判断
    • 2.偏序关系剪枝
      • 偏序关系其实就是代表了状态转移的方向
    • 3.记忆化剪枝
      • 记忆化剪枝就是去对应的哈希数组判断这个状态是否曾经已经计算过，如果计算过则直接返回，时间复杂度 O(1)
    • 4.递归计算结果并返回
      • 这一步就是深度优先搜索的递归过程，也是递归子问题取最优解的过程，需要具体问题具体分析

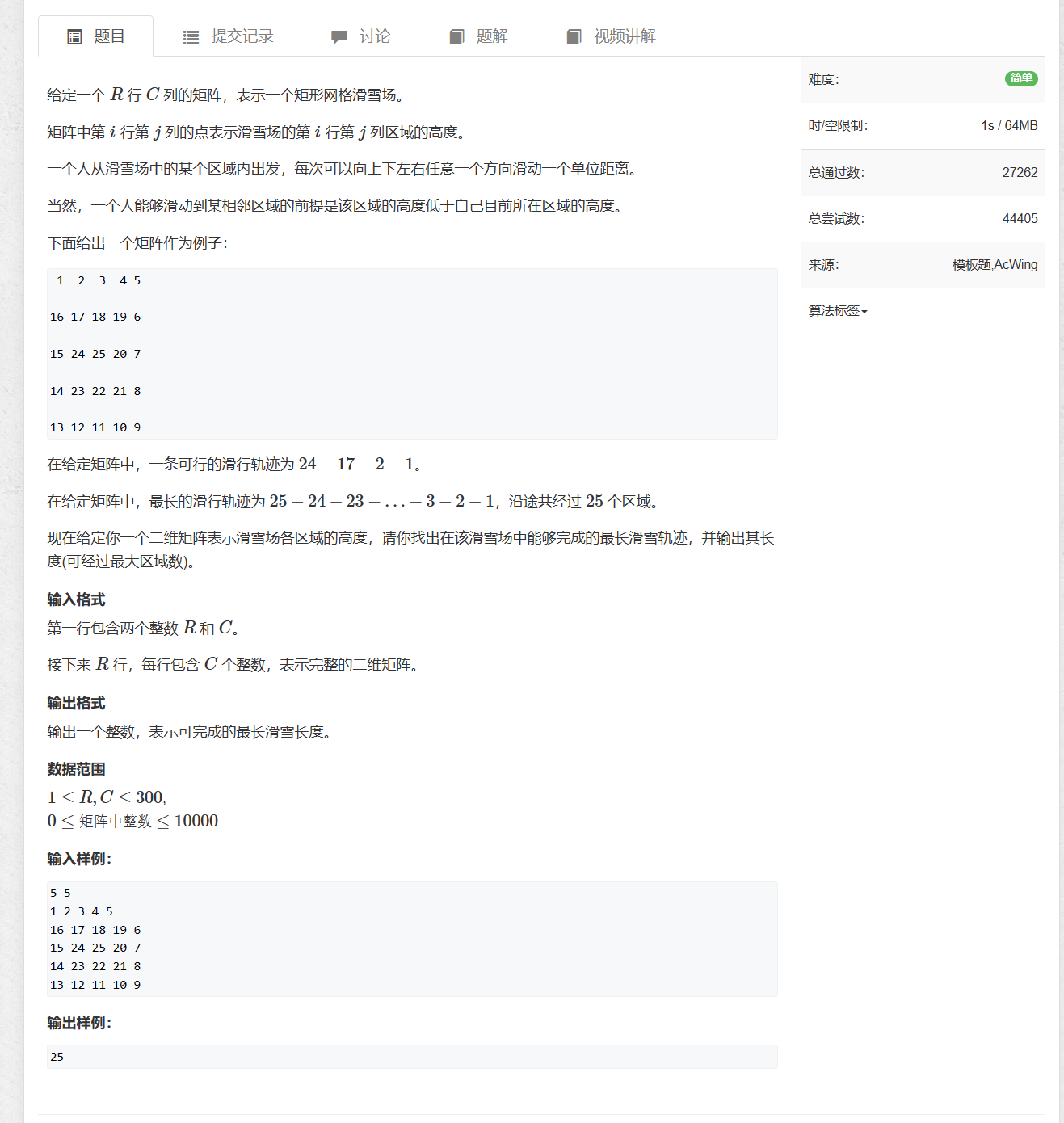
image-20231006191108500

思路：

​ 挨个遍历，求出最大长度。

​ 注意：用dp[x] [y]记录该坐标的最大长度。

​ 每个坐标的最大长度：dp[x] [y] = max(dp[x] [y], findPath(new_x, new_y) + 1);

​ 需要满足新坐标的高度低于当前坐标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <vector>
#include <cstring>

using namespace std;

const int N = 310;
int row, col;
int h[N][N];
int dx[4] = {0, -1, 0, 1};
int dy[4] = {1, 0, -1, 0};
int dp[N][N];

int findPath(int x, int y){
    // 记忆化搜索
    if(dp[x][y] != -1){
        return dp[x][y];
    }
    dp[x][y] = 1;
    for(int i = 0; i < 4; i++){
        int new_x = x + dx[i];
        int new_y = y + dy[i];
        if(new_x < 0 || new_x >= row || new_y < 0 || new_y >= col || h[new_x][new_y] >= h[x][y]){
            continue;
        }
        dp[x][y] = max(dp[x][y], findPath(new_x, new_y) + 1);
    }
    return dp[x][y];
}

int main(){
    scanf("%d%d",&row, &col);
    for(int i = 0; i < row; i++){
        for(int j = 0; j < col; j++){
            scanf("%d", &h[i][j]);
        }
    }
    memset(dp, -1, sizeof(dp));
    int ret = 0;
    for(int i = 0; i < row; i++){
        for(int j = 0; j < col; j++){
            ret = max(ret, findPath(i, j));
        }
    }
    printf("%d\n", ret);
    return 0;
}

最长相邻不相等子序列

image-20231017132110897

思路：

​ 题目要求比较繁杂，如果正常思路挨个考虑，基本不可能实现。所以用动态规划

​ 从后往前遍历，记录以每个节点开始的最大子序列长度，另外需要开辟一个数组记录此节点的上一个元素坐标

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
public:
    // 主函数
    vector<string> getWordsInLongestSubsequence(int n, vector<string>& words, vector<int>& groups) {
        vector<int> dp(n);   // 用于存储以每个单词结尾的最长子序列的长度
        vector<int> from(n); // 用于跟踪子序列的来源
        int mx = n - 1;      // 用于记录最长子序列的最后一个单词的索引

        // 从最后一个单词开始向前遍历
        for (int i = n - 1; i >= 0; i--) {
            for (int j = i + 1; j < n; j++) {
                // 如果当前单词比之前的某个单词更长的子序列，不属于同一组，并且满足is_ok条件
                if (dp[j] > dp[i] && groups[i] != groups[j] && is_ok(words[i], words[j])) {
                    dp[i] = dp[j];    // 更新以当前单词结尾的子序列长度
                    from[i] = j;      // 记录子序列的来源（前一个单词的索引）
                }
            }
            dp[i]++;    // 当前单词自身也属于子序列
            if (dp[i] > dp[mx]) {
                mx = i;   // 更新最长子序列的结束单词索引
            }
        }

        int m = dp[mx];   // 最长子序列的长度
        vector<string> ans(m); // 用于存储最长子序列的单词

        for (int i = 0; i < m; i++) {
            ans[i] = words[mx]; // 存储当前单词
            mx = from[mx];      // 获取下一个单词的索引（子序列来源）
        }

        return ans; // 返回具有最长子序列的单词向量
    }

    // 辅助函数，用于检查两个单词是否只有一个字符不同
    bool is_ok(string& s, string& t) {
        if (s.size() != t.size()) {
            return false;
        }
        bool diff = false;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] != t[i]) {
                if (diff) {
                    return false;
                }
                diff = true;
            }
        }
        return diff;
    }
};

使数组变美的最小增量

image-20231101103259515

思路：动态规划,记忆化搜索

考虑最后一个元素选或不选

​ 若选，将该数增大至k，对于左边那个数，右边就有一个k；

​ 若不选，对于左边那个数，右边没有满足条件的数

同样，对于倒数第二个数

​ 若选，将该数增大至k，对于倒数第三个数，右边就有一个k；

​ 若不选，对于倒数第三个数，右边的2个数均布满足条件，所以该数必须选，即增大至k。(不考虑右边两个数是否大于k,在函数中会判断)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    long long minIncrementOperations(vector<int>& nums, int k) {
       int n = nums.size();
       vector<vector<long long>> v(n, vector<long long>(3, -1));
       // function创建函数对象 long long是返回值类型(int, int)是参数列表
       function<long long(int, int)> dfs = [&](int i, int j)-> long long{
            if(i < 0){
                return 0;
            }
            auto& ret = v[i][j];
            if(ret != -1){
                return ret;
            }
            // 考虑增大i
            ret = dfs(i - 1, 0) + max(k - nums[i], 0);
            if(j < 2){
                // 可以不增大i
                ret = min(ret, dfs(i - 1, j + 1));
            }
            return ret;
       };
       return dfs(n - 1, 0);
    }
};

和为目标值的最长子序列

image-20231105115611535

思路：经典的01背包问题

  • dp[i]：表示值为i时最大子序列的长度
  • 用s记录和的最大值,不能大于target
    • 循环遍历s到当前值，记录这区间内能得到的长度的最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
 class Solution {
public:
    int lengthOfLongestSubsequence(vector<int>& nums, int target) {
        // 创建一个动态规划数组 dp，dp[i] 表示和为 i 的最长子序列的长度
        vector<int> dp(target + 1, INT_MIN); // 初始化为负无穷，表示不可达
        dp[0] = 0; // 和为 0 的子序列长度为 0
        int s = 0; // 记录当前和的最大值

        for(auto x : nums) {
            // 更新 s 为当前和 s 加上当前元素 x，但不超过 target
            s = min(s + x, target);

            // 从当前和 s 递减到 x，更新 dp 数组
            for(int j = s; j >= x; j--) {
                dp[j] = max(dp[j], dp[j - x] + 1);
            }
        }
        
        // 如果 dp[target] 大于 0，表示存在和为 target 的子序列，返回其长度
        // 否则返回 -1 表示无法找到子序列
        return dp[target] > 0 ? dp[target] : -1;
    }
};

树形DP

基本案例

image-20231106204829184

树形dp的基本思路：使用后序遍历，因为该层节点的值的处理逻辑需要下一层的结果作为中间值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int rob(TreeNode* root) {
        // 0表示不选, 1表示选
        vector<int> ret = rob_tree(root);
        return max(ret[0], ret[1]);
    }

    vector<int> rob_tree(TreeNode* cur){
        if(cur == nullptr){
            return vector<int>{0, 0};
        }
        // 后序遍历
        vector<int> left = rob_tree(cur->left);
        vector<int> right = rob_tree(cur->right);
        // 处理当前节点逻辑
        // 选
        int val = cur->val + left[0] + right[0];
        // 不选
        int non_val = max(left[0], left[1]) + max(right[0], right[1]);
        return vector<int>{non_val, val};
    }
};

贪心算法

理论基础

贪心没有固定套路

通过局部最优，推出整体最优

  • 贪心的四个步骤：
    • 将主问题拆分为子问题
    • 找出合适的贪心策略
    • 求解每一个子问题的最优解
    • 将局部最优解堆叠成全局最优解

将钱分给最多的儿童

image-20230922101152832

这段代码采用了一种贪心的逻辑来尽可能均匀地分配钱给孩子。其逻辑如下：

  1. 首先，检查是否有足够的钱来分给每个孩子。如果钱不足以分给每个孩子，就返回-1，表示无法分配。

  2. 然后，每个孩子应得的1块钱会从总金额中扣除，以确保每个孩子至少能得到1块钱。

  3. 接下来，尽可能多地分配7块钱给孩子，以确保余下的钱尽可能均匀地分配。计算最多可以分给多少个孩子7块钱，并将相应数量的钱从总金额中扣除。

  4. 最后，如果还有余下的钱且只剩一个孩子，但余下的钱不足以分给这个孩子，它会减少一个可以分到7块钱的孩子，以确保余下的钱均匀分配。

这种方法的目标是尽可能多地分配7块钱，以确保孩子获得尽可能多的钱，同时保持余下的钱均匀分配。这种贪心策略可以有效地满足问题的要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int distMoney(int money, int children) {
        // 如果钱不足以分给每个孩子，返回-1
        if (money < children) {
            return -1;
        }
        
        // 减去每个孩子应得的1块钱，以确保每个孩子至少能得到1块钱
        money -= children;
        
        // 计算最多可以分给多少个孩子7块钱，这样剩余的钱尽可能均匀分给孩子
        int cnt = min(money / 7, children); // 多少个人可以分到7
        money -= cnt * 7; // 减去分给孩子的7块钱
        children -= cnt; // 更新剩余的孩子数量
        
        // 如果还有余下的钱且只剩一个孩子，但余下的钱不足以分给这个孩子，减少一个可以分到7块钱的孩子
        if (children == 0 && money > 0 || children == 1 && money == 3) {
            cnt--;
        }
        
        // 返回最多可以分到7块钱的孩子数量
        return cnt;
    }
};

最大子序和

image-20230923150701955

思路：使用贪心

​ 局部最优：每加一次与最大值进行判断，如果大于最大值则更新最大值。若相加之后小于零，说明这个数已经比之前的子序列和小了，而且之后也不需要加上他的子序列(因为现在是小于零的)，所以重置为0，再计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
private:
    int sum = INT_MIN;
public:
    int maxSubArray(vector<int>& nums) {
        int tmp = 0;
        for(const auto& i : nums){
            tmp += i;
            sum = max(sum, tmp);
            if(tmp < 0){
                tmp = 0;
            }
        }
        return sum;
    }
};

合并区间

image-20230923153507870

算法：

​ 判断前一个元素第二个值是否与该元素的第一个值重合，若重合则更新。但是注意，不能直接替换，需要比较两个元素第二个值的大小。比如[1, 4] [2, 3],此时就不需要替换

​ 若没有重合，那么前一个元素确定，将该元素插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> ret;
        sort(intervals.begin(), intervals.end());
        int n = intervals.size();
        ret.push_back(intervals[0]);
        for(int i = 1; i < n; i++){
            if(ret.back()[1] < intervals[i][0]){
                ret.push_back(intervals[i]);
            }else{
               ret.back()[1] = max(intervals[i][1], ret.back()[1]); 

            }
        }
        return ret;
    }
};

一手顺子

image-20231011172739924

思路：

​ 使用贪心的思维。利用一个map将每张牌出现的次数记录。注意需要对数组从小到大排序，这样才能保证不遗漏顺子。

​ 排序后从头开始遍历，若该元素存在，则数组需要连续存在groupsize个元素，但凡有一个不存在，则表示不满足情况，返回false。每遍历一个需要再map中更新数量。

​ 注意判断，若map中没有数组的元素，说名该元素已经被使用完，跳过该元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
public:
    bool isNStraightHand(vector<int>& hand, int groupSize) {
        int n = hand.size();
        if(n % groupSize != 0){
            return false; // 如果总牌数不能被groupSize整除，无法分组，返回false
        }
        map<int, int> map; // 使用map来统计每种牌的数量
        for(auto i : hand){
            map[i]++;
        }
        sort(hand.begin(), hand.end()); // 对牌进行排序

        for(auto x : hand){
            if(map.count(x) == 0){
                continue; // 如果牌x已被使用完，跳过
            }
            for(int j = 0; j < groupSize; j++){
                int num = x + j;
                if(map.count(num) == 0){
                    return false; // 不能找到连续的牌，返回false
                }
                map[num]--;
                if(map[num] == 0){
                    map.erase(num); // 移除已用完的牌
                }
            }
        }
        return true; // 所有牌都能分组成连续的组，返回true
    }
};

增减字符串匹配

image-20231027153049280

思路：

​ 可以使用贪心算法，当s[i] == I时，说明这个数比下一个数小，将从最小值0开始赋值，赋值之后右移

​ 当s[i] == ‘D’时，说明这个数字比下一个数字大，从最大的数开始赋值，赋值之后左移。

​ 对每一个数都如此判断，最后一个数时两个指针必定汇合

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    vector<int> diStringMatch(string s) {
        int n = s.size();
        int l =0, r = n;
        vector<int> perm(n + 1);
        for(int i = 0; i < n; i++){
            perm[i] = s[i] == 'I' ? l++ : r--;
        }
        perm[n] = l;
        return perm;
    }
};

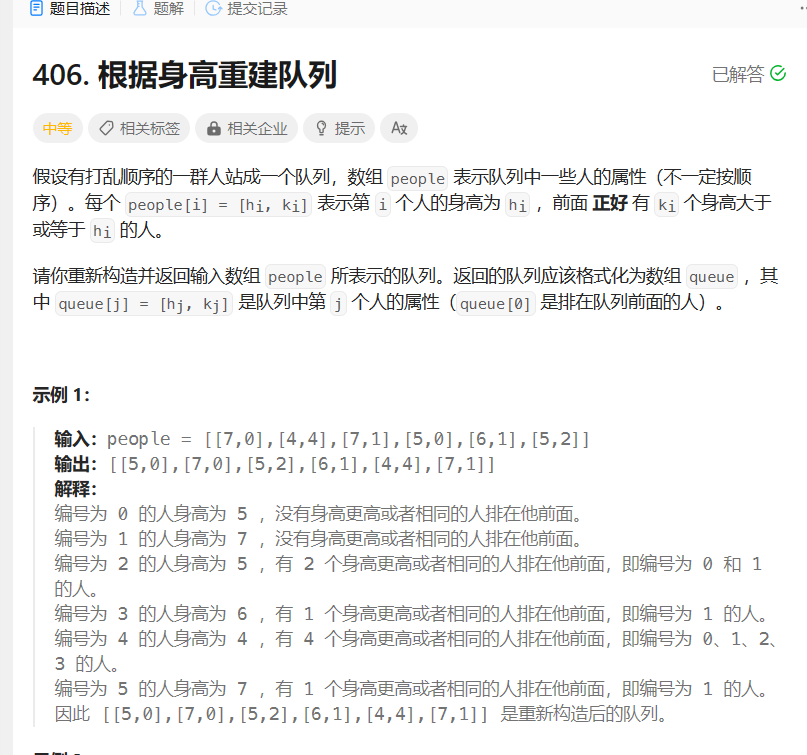
根据身高重建队列

image-20231106102829372

贪心思路

遇到两个维度，若同时考虑，那么总会顾此失彼，先考虑一个维度，再考虑另一个维度。至于如何确定其中一个维度，先看确定它是否能确定一种规律。在本题中，若先考虑”有多少人在其之前”这个维度，那么什么都确定不了。若先考虑身高，按身高降序排列，那么至少能确定该元素之前的身高都比其高，可以优先插入前面的元素。这样思路就出来了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        // 先确定身高维度
        sort(people.begin(), people.end(), [](auto a, auto b){
            if(a[0] == b[0]){
                return a[1] <b[1];
            }
            return a[0] > b[0];
        });
        // 链表插入效率更高
        list<vector<int>> ret;
        for(int i = 0; i < people.size(); i++){
            int pos = people[i][1];
            list<vector<int>>::iterator iter = ret.begin();
            while(pos--){
                iter++;
            }
            ret.insert(iter,people[i]);
        }
        return vector<vector<int>>(ret.begin(), ret.end());
    }
};

分发糖果

​ image-20231106104353651

还是老问题：题中有左右两个维度，若同时考虑，肯定会顾此失彼。所以先考虑一个维度在考虑另一个维度。这里考虑左边比右边大和右边比左边大都可以，两者是等价的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int candy(vector<int>& ratings) {
        int cnt = 1;
        int n = ratings.size();
        // 记录左边小于右边的值
        vector<int> less(n,1);
        // 记录左边大于右边的值
        vector<int> greater(n,1);
        for(int i = 1; i < n; i++){
            if(ratings[i] > ratings[i - 1]){
                less[i] = less[i - 1] + 1;
            }
        }
        for(int i = n - 2; i >= 0; i--){
            if(ratings[i] > ratings[i + 1]){
                greater[i] = greater[i + 1] + 1;
            }
        }
        int ret = 0;
        for(int i = 0; i < n; i++){
            if(less[i] < greater[i]){
                ret += greater[i];
            }else{
                ret += less[i];
            }
        }
        return ret;
    }
};

监控二叉树

image-20231106113542724

该题也可以用dp做。现在介绍贪心。

  • 要使摄像头数量最少，那么根节点和叶子节点不能按摄像头
  • 从上往下考虑情况过于复杂，考虑从下往上遍历。如何从下往上遍历呢？后序遍历
  • 用1 2 0分别表示此处加摄像头，此处被覆盖和此处没有被覆盖
  • 为了满足第一个条件，空节点默认为状态2，即被覆盖
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
	/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int ret;
    
    int traversal(TreeNode* cur){
        if(cur == nullptr){
            return 2;
        }
        // 记录左儿子的状态
        int left = traversal(cur->left);
        // 记录右儿子的状态
        int right = traversal(cur->right);
        if(left == 2 && right == 2){
            // 左右儿子均被覆盖但没有摄像头,说明该节点未被覆盖
            return 0;
        }else if(left == 0 || right == 0){
            // 左右孩子有一个未被覆盖,该节点必须加摄像头
            ret++;
            return 1;
        }else{
            // 左右孩子至少有一个摄像头
            return 2;
        }
    }
public:
    int minCameraCover(TreeNode* root) {
        ret = 0;
        if(traversal(root) == 0){
            // 根节点未被覆盖,必须加上摄像头
            ret++;
        }
        return ret;
    }
};

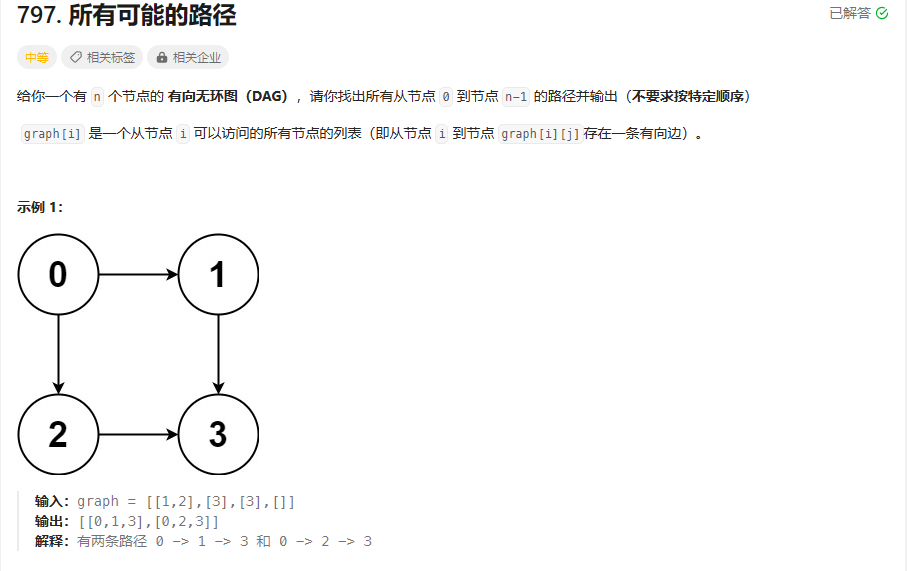
dfs

所有可能的路径

image-20230924154642842

思路：这是一道最常规的深度优先搜索算法。因为题目告诉你是有向无环图，不存在回路，所以无脑深搜就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
private:
    vector<vector<int>> ret;
    vector<int> tmp;
    int n;
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        n = graph.size();
        tmp.push_back(0);
        dfs(graph, 0);
        return ret;
    }

    void dfs(vector<vector<int>>& graph, int index){
        if(index == n - 1){
            ret.push_back(tmp);
            return;
        }
        for(int i = 0; i < graph[index].size(); i++){
            tmp.push_back(graph[index][i]);
            dfs(graph, graph[index][i]);
            tmp.pop_back();
        }
    }
};

N皇后

image-20230926112419552

思路：实质上是深度优先搜索(回溯)

​ 难点是如何判断对角线是否访问过
​ 用dg 和 udg数组来记录访问

​ dg[x + y] 和udg[x + n - y]分别代表正对角线和反对角线是否访问过

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
private:
    vector<bool> row;
    vector<bool> col;
    vector<bool> dg;
    vector<bool> udg;
    vector<vector<string>> ret;
    vector<string> d;
    int N;
public:
    vector<vector<string>> solveNQueens(int n) {
        N = n;
        row.resize(n, false); 
        col.resize(n, false); 
        dg.resize(2 * n, false); 
        udg.resize(2 * n, false); 
        string s;
        for(int i = 0; i < n; i++){
            s += '.';
        }       
        for(int i = 0; i < n; i++){
            d.push_back(s);
        }
        vector<string> ans;
        dfs(0,ans);
        return ret;
    }
    void dfs(int index, vector<string> ans){
        if(index == N){
            ret.push_back(ans);
            return;
        }
        for(int j = 0; j < N; j++){
            if(col[j] == false && row[index] == false && dg[j + index] == false && udg[index + N - j] == false){
                col[j] = true;
                row[index] == true; 
                dg[j + index] = true;
                udg[index + N - j] = true;
                d[index][j] = 'Q';
                ans.push_back(d[index]);
                dfs(index + 1, ans);
                ans.pop_back();
                col[j] = false;
                row[index] == false; 
                dg[j + index] = false;
                udg[index + N - j] = false;
                d[index][j] = '.';
            }
        }
    }
};

bfs

岛屿数量

image-20230924160823517

思路：这是一道最基本的宽度优先搜索。找到连续的’1’，具体实现时需要注意如何判断是同一片，我用了flags和visited来记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
private:
    int cnt = 0;
    vector<vector<bool>> visited;
    int row;
    int col;
    int dx[4] = {1, 0, -1, 0};
    int dy[4] = {0, -1, 0, 1};
    bool flag = false;
public:
    int numIslands(vector<vector<char>>& grid) {
        row = grid.size();
        if(row == 0){
            return 0;
        }
        col = grid[0].size();
        visited.resize(row, vector<bool>(col, false));
        for(int i = 0; i < row; i++){
            for(int j = 0; j < col; j++){
                flag = false;
                bfs(grid, i , j);
                if(flag){
                    cnt++;
                }
            }
        }
        return cnt;
    }

    void bfs(vector<vector<char>>& grid, int x, int y){
        if(grid[x][y] == '0' || grid[x][y] == true){
            return;
        }
        flag = true;
        grid[x][y] = true;
        for(int i = 0; i < 4; i++){
            int new_x = x + dx[i];
            int new_y = y + dy[i];
            if(new_x < 0 || new_x >= row || new_y < 0 || new_y >= col){
                continue;
            }
            bfs(grid, new_x, new_y);
        }
    }
};

双指针

链表相交

image-20230925074522227

思路：

​ 此题大致思路是挨个比较，返回第一个值相等的元素。

​ 问题：如何解决长度不一样的问题

​ 观察图形发现，只要一个元素地址相等，之后相当于是同一个链表(链表的结构所决定)，相等之后的长度一定是一样的，我们只需要将长度更长的那一个链表向前移动两者长度之差即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int lenA = 0;
        int lenB = 0;
        ListNode* tmp = headA;
        while(tmp != nullptr){
            tmp = tmp->next;
            lenA++;
        }
        tmp = headB;
        while(tmp != nullptr){
            tmp = tmp->next;
            lenB++;
        }
        if(lenA > lenB){
            int len = lenA - lenB;
            while(len > 0){
                headA = headA->next;
                len--;
            }
        }else if(lenA < lenB){
            int len = lenB - lenA;
            while(len > 0){
                headB = headB->next;
                len--;
            }
        }

        while(headA != nullptr){
                if(headA == headB){
                    return headA;
                }
                headA = headA->next;
                headB = headB->next;
        }
        
        return headA;
    }
};

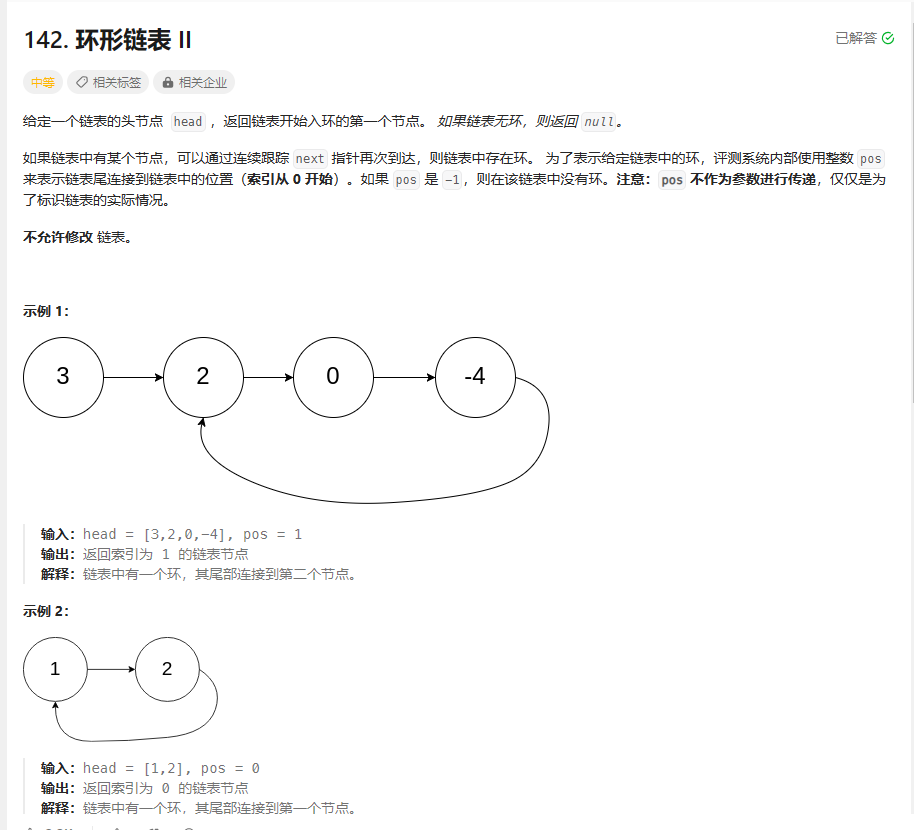
环形链表

思路：这道题使用双指针解决

​ 具体逻辑其实是通过数学计算得出的 ，假设从起点到入口有a个节点，环内有b个节点

  • 有以下关系(slow走了f步)
    • 快指针每次走的步数是慢指针的2倍， fast 走了 2s 步 slow 走了s 步
    • 相遇时，fast比slow多走了n圈，fast = s + nb slow = s
  • 解出 slow = nb ,fast = 2nb
  • 之后怎么计算出入口呢？
    • 已知起点到入口可以走a + nb步路 (n >= 0)
    • 那么slow需要向前走a步即到达入口。但是怎么确定a呢
    • 不要忘记初始节点到入口的距离就是a，所以只需要找一个指针从初始节点开始走，当两节点相遇时即为入口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(true){
            if(fast == nullptr || fast->next == nullptr){
                return nullptr;
            }
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow){
                break;
            }
        }
        fast = head;
        while(slow != fast){
            slow = slow ->next;
            fast = fast->next;
        }
        
        return slow;
    }
};

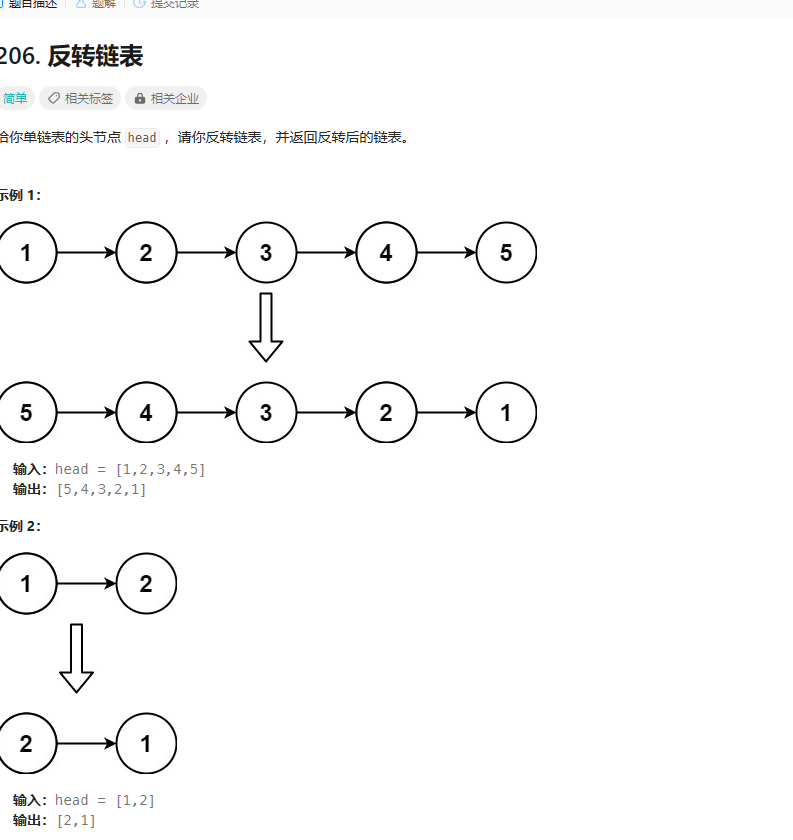
翻转链表

image-20230926102756078

思路：

​ 定义三个指针，pre代表前一个，cur代表当前，next代表下一个

​ 具体如何操作：画图观察，翻转链表，即当前元素的下一个元素需要指向现在元素的前一个节点。 cur->next = pre;

​ 现在需要向后移，即pre = cur

​ cur = next; next = cur->next;

​ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head == nullptr || head->next == nullptr){
            return head;
        }
        ListNode* pre = nullptr;
        ListNode* cur = head;
        ListNode* next = head->next;
        while(cur != nullptr){
            next = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next;
        }
        return pre;
    }
};

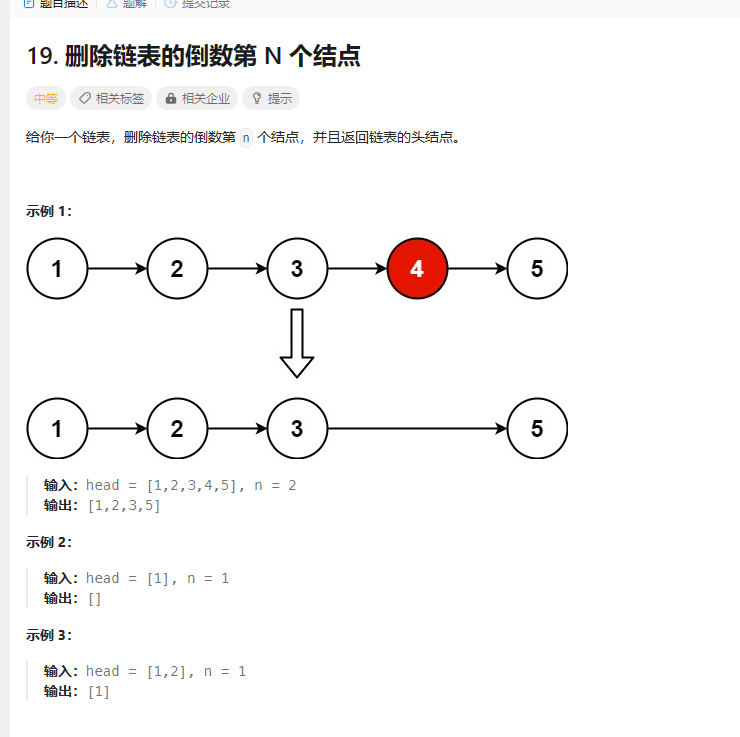
删除链表倒数第N个节点

image-20230926104635639

思路：

​ 先进行一次遍历求出链表长度，在计算要删除的倒数第N个节点具体位置

​ 删除思路：先判断是否是头结点，若是，直接返回下一个节点即可。若不是，移动到要删除的节点的上一个节点，node->next = node->next->next

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        int len = 0;
        ListNode* tmp = head;
        while(tmp != nullptr){
            tmp = tmp->next;
            len++;
        }
        len -= n;
        if(len == 0){
            return head->next;
        }
        tmp = head;
        while(len > 1){
            tmp = tmp->next;
            len--;
        }
        tmp->next = tmp->next->next;
        return head;
    }
};

比较版本号

image-20231008223413748

思路：

​ 使用双指针，在每个区间内比较两数大小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int compareVersion(string version1, string version2) {
        int n = version1.size(), m = version2.size();
        int i = 0, j = 0;
        while(i < n || j < m){
            long x = 0;
            for(; i < n && version1[i] != '.'; i++){
                x = x * 10 + version1[i] - '0';
            }
            i++;
            long y = 0;
            for(; j < m && version2[j] != '.'; j++){
                y = y * 10 + version2[j] - '0';
            }
            j++;
            if(x != y){
                return x > y ? 1 : -1;
            }
        }
        return 0;
    }
};

搜索旋转数组

image-20231009142638630

思路：

​ 基本思路还是使用双指针。但是需要注意数组不是纯有序的

​ 当中间值与目标值相同时，返回true

​ 当中间值和左右两边相同时，不能判断目标值在哪边，左端点++ 右端点– 缩小范围

​ 当左边值小于等于中间值时(左半段有序)，分成两种情况

​ nums[l] <= target && target < nums[mid]，说明左边到中间是有序的并且目标值在这一范围。更新

​ 右端点r = mid - 1

​ 否则目标值在右半部分，更新左端点 l = mid + 1

​ 当中间值大于左端点值时(右半段有序)，分成两种情况

​ nums[mid] < target && target <= nums[r]说明目标值在右半段，更新左指针

​ 其余情况说明在左半段

  • 此题精妙之处在于摈弃了复杂的半段，在左右半边分别都只判断了一种简单的情况，因为target不在左半边就在右半边，另一种情况直接用else即可。
  • 为什么需要nums[l] == nums[mid] && nums[r] == nums[mid]，因为数组中有重复的值，可能造成无法判断大小的情况
  • 没有重复元素的情况更简单，具体参考力扣33题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1; // 初始化左右指针，用于定义搜索范围

        while (l <= r) { // 当左指针小于等于右指针时，继续搜索
            int mid = ((r - l) >> 1) + l; // 计算中间位置

            if (nums[mid] == target) { // 如果中间值等于目标值，找到目标，返回true
                return true;
            }

            // 处理可能存在的重复元素情况
            if (nums[l] == nums[mid] && nums[r] == nums[mid]) {
                l++;
                r--;
            } else if (nums[l] <= nums[mid]) { // 左半段是有序的情况
                if (nums[l] <= target && target < nums[mid]) {
                    r = mid - 1; // 目标值在左半段，更新右指针
                } else {
                    l = mid + 1; // 目标值在右半段，更新左指针
                }
            } else { // 右半段是有序的情况
                if (nums[mid] < target && target <= nums[r]) {
                    l = mid + 1; // 目标值在右半段，更新左指针
                } else {
                    r = mid - 1; // 目标值在左半段，更新右指针
                }
            }
        }
        return false; // 未找到目标值，返回false
    }
};

找出满足差值条件的下标

image-20231016085415527

思路

​ 使用双指针+维护最大最小值

​ 在枚举j的同时，维护nums[i]的最大值和最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> findIndices(vector<int>& nums, int indexDifference, int valueDifference) {
        int max_idx = 0, min_idx = 0;
        int n = nums.size();
        for(int j = indexDifference; j < n; j++){
            int i = j - indexDifference;
            if(nums[i] > nums[max_idx]){
                max_idx = i;
            }
            if(nums[i] < nums[min_idx]){
                min_idx = i;
            }
            if(nums[max_idx] - nums[j] >= valueDifference){
                return {max_idx, j};
            }
            if(nums[j] - nums[min_idx] >= valueDifference){
                return {min_idx, j};
            }
        }
        return {-1,-1};
    }
};

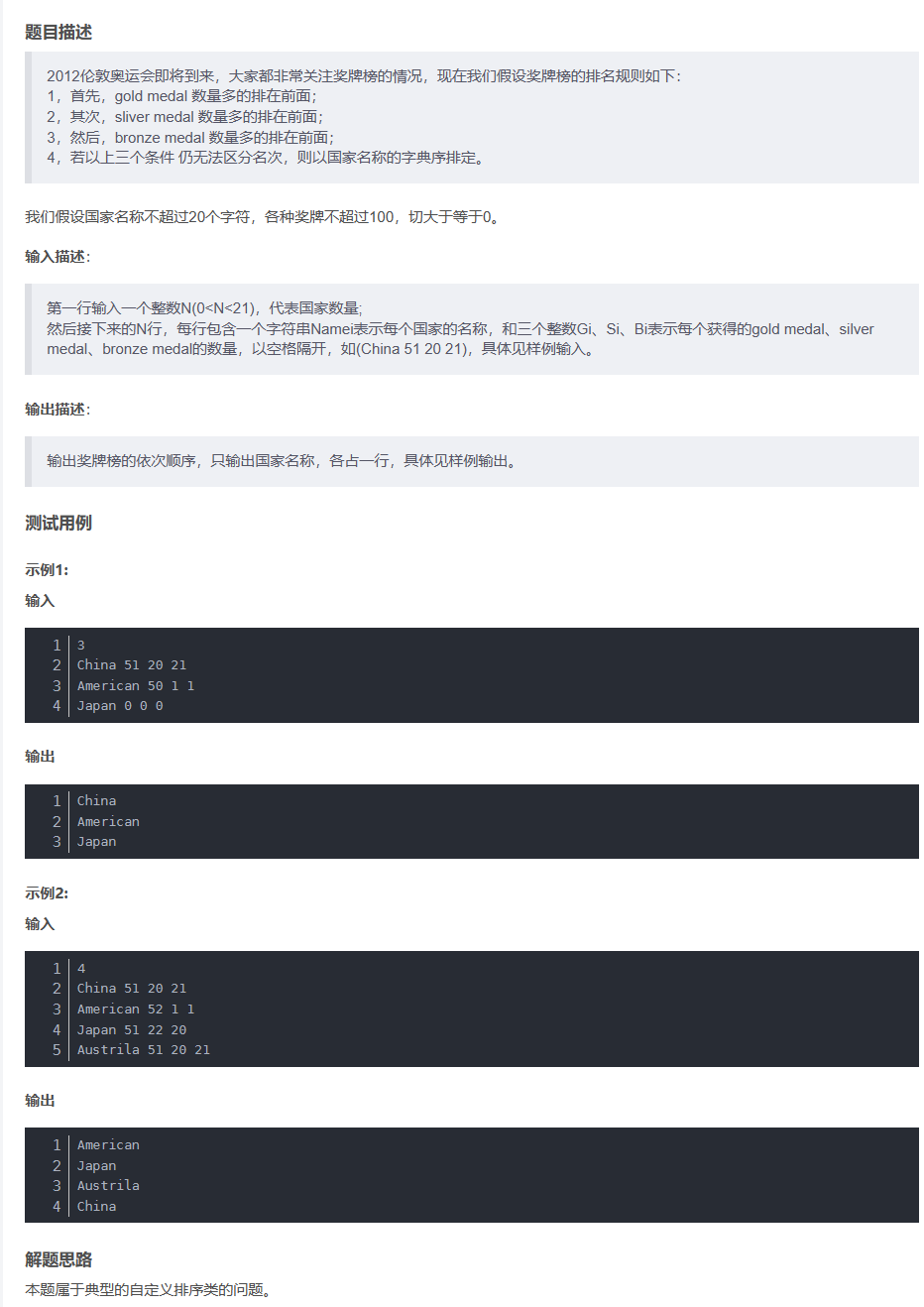
多关键字自定义排序

华为机考

image-20230925200607228

第一次接触这种题，思路如下：

​ 因为是多关键字排序，每个关键字对排序都会有影响。那么需要将关键字之间存储起来以备后用，此时想到用类，将关键字声明为成员变量。

​ 首先将其存储起来，用vector数组，然后我们需要对数组进行排序，这里使用sort，第三个参数定义为回调函数，我自定义了一个函数，一个是lambda表达式，一个是函数式。函数实现内容是题目要求排队方式

​ 注意transform函数，这个函数会前两个参数是迭代器，表示遍历范围，第三个参数也是迭代器，若返回容器.begin则代表覆盖该容器的元素，若是容器.end则代表重新开辟一块内存。建议使用后者。

​ tolower()只能传入一个字符，返回其小写形式，::代表作用域，左边空着表示全局作用域。

我给了两种实现，如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
// #include <algorithm>
// #include <iostream>
// #include <string>
// #include <vector>

// using namespace std;

// int n;

// class Record {
// public:
//     string m_country;
//     int m_Gi;
//     int m_Si;
//     int m_Bi;
//     Record(string mCountry, int mGi, int msi, int mBi) : m_country(mCountry), m_Gi(mGi), m_Si(msi), m_Bi(mBi) {}
// };
// bool myCompare(Record& record1, Record& record2) {
//     // 先按照金牌排序
//     if (record1.m_Gi != record2.m_Gi) {
//         return record1.m_Gi > record2.m_Gi;
//     } else if (record1.m_Si != record2.m_Si) {
//         return record1.m_Si > record2.m_Si;
//     } else if (record1.m_Bi != record2.m_Bi) {
//         return record1.m_Bi > record2.m_Bi;
//     } else {
//         string country1 = record1.m_country;
//         string country2 = record2.m_country;
//         transform(country1.begin(), country1.end(), country1.end(), ::tolower);
//         // transform(country2.begin(), country2.end(), country2.end(), ::tolower);
//         transform(country2.begin(), country2.end(), country2.end(), [](char c) {
//             return tolower(c);
//         });
//         return country1.compare(country2);
//     }
// }

// void myPrint(Record& record) {
//     cout << record.m_country << endl;
// }

// int main() {
//     cin >> n;
//     vector<Record> v;
//     v.reserve(n);
//     for (int i = 0; i < n; i++) {
//         string country;
//         int gold, silver, copper;
//         cin >> country >> gold >> silver >> copper;
//         Record record(country, gold, silver, copper);
//         v.push_back(record);
//     }
//     sort(v.begin(), v.end(), myCompare);
//     for (auto vec : v) {
//         myPrint(vec);
//     }
//     return 0;
// }

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;
int n;

class Record {
public:
    string m_country;
    int m_gold;
    int m_sliver;
    int m_bronze;
    Record(string country, int gold, int sliver, int bronze) : m_country(country), m_gold(gold), m_sliver(sliver), m_bronze(bronze) {}
};

int main() {
    cin >> n;
    vector<Record> v;
    v.reserve(n);
    for (int i = 0; i < n; i++) {
        string country;
        int gold, sliver, bronze;
        cin >> country >> gold >> sliver >> bronze;
        Record record(country, gold, sliver, bronze);
        v.push_back(record);
    }
    sort(v.begin(), v.end(), [](auto r1, auto r2) -> bool {
            if (r1.m_gold != r2.m_gold) {
                return r1.m_gold > r2.m_gold;
            } else if (r1.m_sliver != r2.m_sliver) {
                return r1.m_sliver > r2.m_sliver;
            } else if (r1.m_bronze != r2.m_bronze) {
                return r1.m_bronze > r2.m_bronze;
            } else {
                string c1 = r1.m_country;
                string c2 = r2.m_country;
                transform(c1.begin(), c1.end(), c1.end(), ::tolower);
                transform(c2.begin(), c2.end(), c2.end(), ::tolower);
                return c1.compare(c2);
            }
        });
        for (auto vec : v) {
            cout << vec.m_country << endl;
        }
        return 0;
}

Trie前缀树

高效的插入和查找一个字符串

  • 适用字符串、二进制需要挨个遍历的结构中

image-20231105211442743

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 100010;
// N层节点(N为字符串的最大长度),每层节点最多向外连接26条边(小写英文字母)
int son[N][26];
// 以当前这个点结尾的单词有多少个
int cnt[N];
int idx = 0; // 当前用到的下标,下标为0的点既是根节点又是空节点
char str[N];

void insert(char str[]){
    // 记录下标
    int p = 0;
    for(int i = 0; str[i]; i++) {
        int u = str[i] - 'a';
        if(!son[p][u]){
            son[p][u] = ++idx;
        }
        p = son[p][u];
    }
    cnt[p]++;
}

int query(char str[]){
    int p = 0;
    for(int i = 0; str[i]; i++){
        int u = str[i] - 'a';
        if(!son[p][u]){
            return 0;
        }
        p = son[p][u];
    }
    return cnt[p];
}

int main(){
    int n;
    memset(son, 0, sizeof(son));
    scanf("%d", &n);
    while(n--){
        char op[2];
        scanf("%s%s", op, str);
        if(op[0] == 'I'){
            insert(str);
        }else {
            printf("%d\n",query(str));
        }
    }
    
    return 0;
}

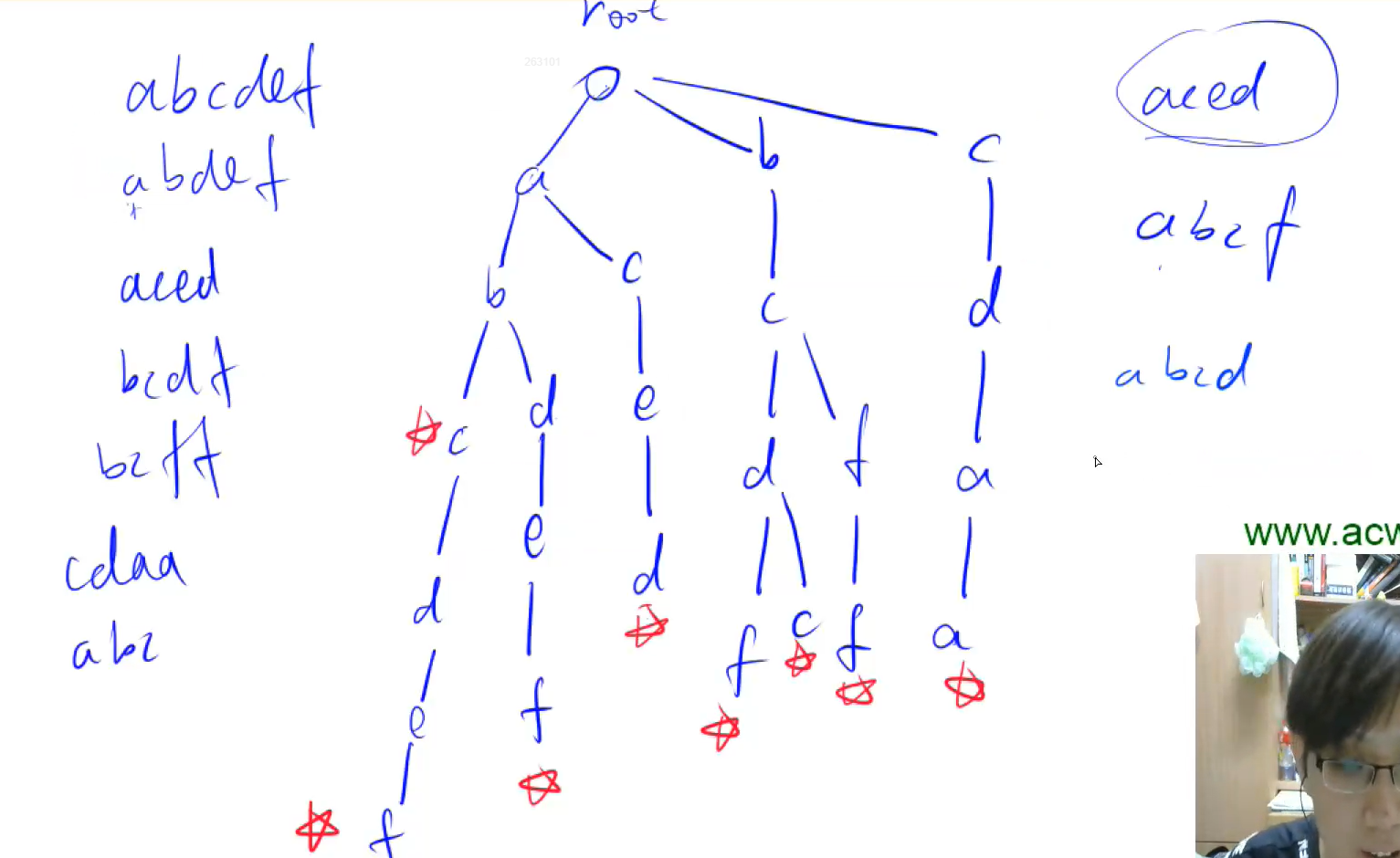
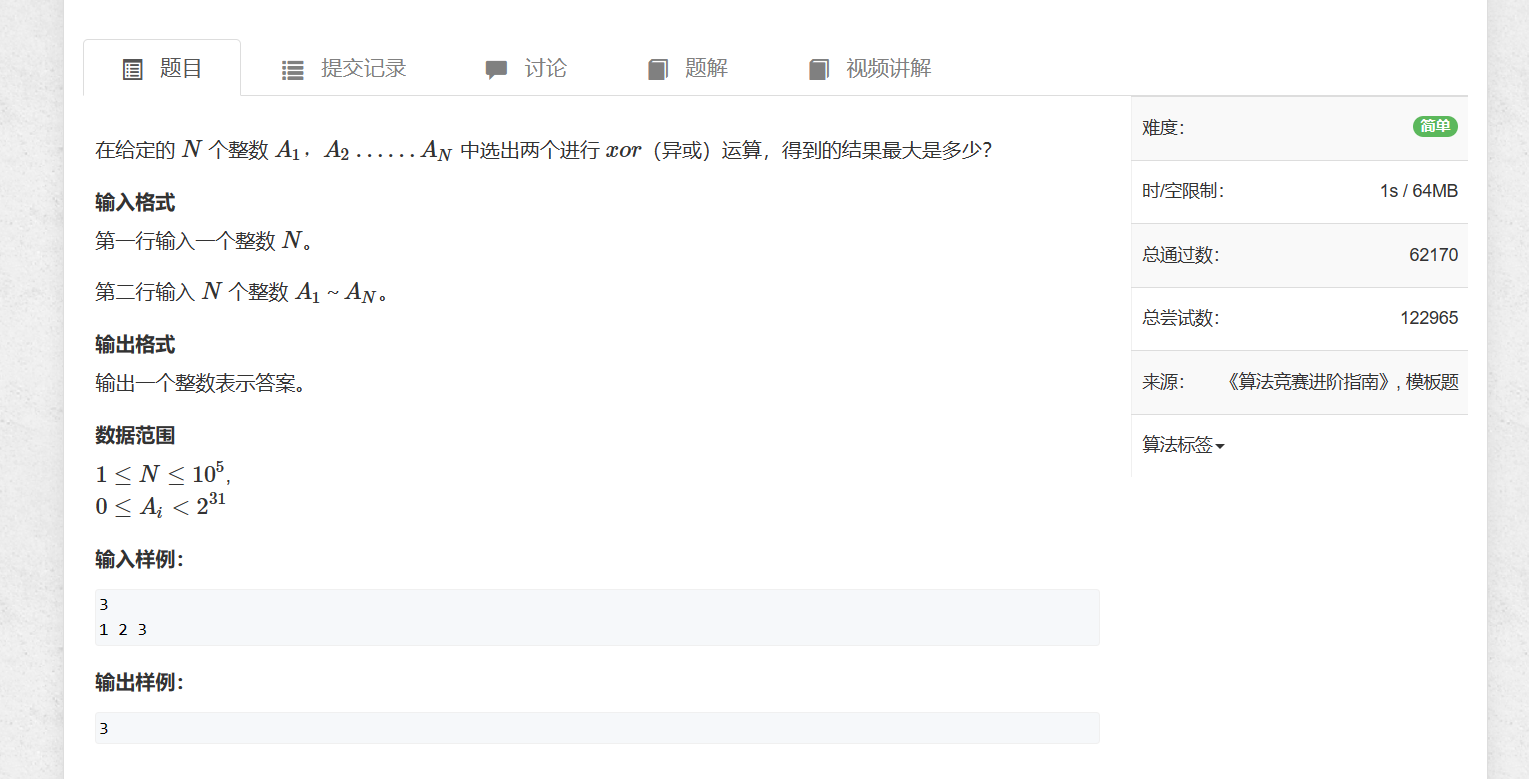
最大异或数

image-20231109085923757

思路：

  • 本题最先想到的肯定是暴力搜索，但是时间复杂度是o(N²),导致超时
  • 使用tire前缀树
    • 由高位到地位分别存取每一位数
    • 从最高位开始遍历，找到与当前位的值相反的节点是否存在。若存在，对结果+ 1 << i，走相反的节点到下一位;若不存在，走对应的节点到下一位(1走0,0走1)
    • 这样时间复杂度就能有效的缩短为O(mn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
#include <cstring>

using namespace std;

// N代表个数、M代表trie的节点个数
const int N = 100010, M = 3000010;
int idx;
int a[N], son[M][2];

void insert(int x){
    // 表示层数
    int p = 0;
    for(int i = 30; i >= 0; i--){
        // 为什么要 &1: 获取当前位数,若不与1,获取的就不止是当前位数
        if(!son[p][(x >> i) & 1]){
            // 第p层没有符合数x的节点,创建
            son[p][x >> i & 1] = ++idx;
        }
        p = son[p][x >> i & 1];
    }
}

int query(int x){
    int p = 0;
    int ret = 0;
    for(int i = 30; i >= 0; i--){
        if(son[p][!(x >> i & 1)]){
            // 存在与该为相反的值
            ret += 1 << i;
            p = son[p][!(x >> i & 1)];
        }else{
            p = son[p][x >> i & 1];
        }
    }
    return ret;
    
}


int main(){
    idx = 0;
    memset(son, 0, sizeof(son));
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &a[i]);
        insert(a[i]);
    }
    int ret = 0;
    for(int i = 0; i < n; i++){
        ret = max(ret, query(a[i]));
    }
    cout << ret <<endl;
    return 0;
}

二叉树

平衡二叉树

image-20230927145232634

思路：

  • 1.自顶向下
    • 每个节点的高度等于左右字节点高度最大值 + 1；
    • 递归遍历每个节点，看每个节点是否都满足要求
  • 2.自底向上
    • 对于每个节点，height只调用一次(自顶下下会重复调用)
  • 自顶向下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root == nullptr){
            return true;
        }
        return abs(height(root->left)- height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
    int height(TreeNode* root){
        if(root == nullptr){
            return 0;
        }
        return max(height(root->left), height(root->right)) + 1;
    }
};
  • 自底向上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root == nullptr){
            return true;
        }
        return height(root) >= 0;
    }
    int height(TreeNode* root){
        if(root == nullptr){
            return 0;
        }
        int leftHeight = height(root->left);
        int rightHeight = height(root->right);
        if(leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1){
            return -1;
        } 
        return max(height(root->left), height(root->right)) + 1;
    }
};

从中序和后续遍历构造二叉树

image-20230927205158065

思路：使用递归构造，注意判断区间，利用中序遍历和后序遍历的性质：

​ 中序遍历：左中右

​ 后续遍历：左右中，后续遍历序列的最后一个元素即为当前字构造根节点的值，再在中序遍历中找到该值，值左边元素即为左子树元素，值右边元素即为右子树元素

使用index哈希表存储中序遍历的元素所在位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    unordered_map<int,int> index;
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        for(int i = 0; i < n; i++){
            index[inorder[i]] = i;
        }
        return mybuild(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
    }

    TreeNode* mybuild(vector<int>& inorder, vector<int>& postorder, int in_begin, int in_end, int post_begin, int post_end){
        if(in_begin > in_end || post_begin > post_end){
            return nullptr;
        }
        TreeNode* root = new TreeNode(postorder[post_end]);
        int cnt = index[postorder[post_end]];
        root->left = mybuild(inorder, postorder, in_begin, cnt - 1, post_begin,post_begin + cnt - in_begin - 1);
        root->right = mybuild(inorder, postorder, cnt + 1, in_end, post_begin + cnt - in_begin, post_end - 1);
        return root;
    }
};

判读平衡二叉树

image-20231012154527732

思路

​ 从上之下逐个判断每个节点是否为平衡的，若不平衡则返回false

​ 在每个节点又需要从该点开始判断其左右子树的高度，返回 该点左右子树的最高高度+1即为该点的高度

为了方便理解：可以用两个函数分别完成上述两个功能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return isVaild(root);
    }
    bool isVaild(TreeNode* root){
        if(root == nullptr){
            return true;
        }
        bool l = isVaild(root->left);
        bool r = isVaild(root->right);
        if(l == false || r == false){
            return false;
        }
        int left = height(root->left);
        int right = height(root->right);
        return abs(left - right) <= 1;
    }
    int height(TreeNode* root){
        if(root == nullptr){
            return 0;
        }
        return 1 + max(height(root->left), height(root->right));
    }
};

哈希表

快乐数

image-20230928150307277

思路：

​ 如何判断无限循环：当出现重复的数时，即能确定该数是无限循环的。这时用一个set集合去存储已经存在的元素，每迭代一次进行一次判断，若该数存在，则返回false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    bool isHappy(int n){
        unordered_set<int> set;
        set.insert(n);
        int sum = n;
        while(1){
            sum = getNum(sum);
            if(sum == 1){
                return true;
            }
            if(set.find(sum) != set.end()){
                return false;
            }
            set.insert(sum);
        }
        return false;
    }

    int getNum(int n){
        int sum = 0;
        while(n){
            sum += (n % 10) * (n % 10);
            n /= 10;
        }
        return sum;
    }
};

LRU缓存

image-20231015221129053

思路：

​ 因为要记录键值对，所以考虑使用哈希表进行存储。

​ 考虑有将元素移动到最前面的需求，所以使用双向链表来设计。靠近头部的节点是最近使用过的节点

​ 设计一个结构体模拟双向链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
// 双向链表
struct DLinkedNode {
    int key, value;
    DLinkedNode* prev;
    DLinkedNode* next;
    DLinkedNode() : key(0), value(0), prev(nullptr), next(nullptr){}
    DLinkedNode(int _key, int _value) : key(_key), value(_value), prev(nullptr), next(nullptr){}
};

class LRUCache {
private:
    // 哈希表存储元素，key为int,value为双向链表
    unordered_map<int, DLinkedNode*>cache;
    // 双向指针模拟顺序
    DLinkedNode* head;
    DLinkedNode* tail;
    int size;
    int capacity;
public:
    LRUCache(int _capacity): capacity(_capacity), size(0) {
        head = new DLinkedNode();
        tail = new DLinkedNode();
        tail->prev = head;
        head->next = tail;
    }
    
    // 取出对应元素的值
    int get(int key) {
        if(!cache.count(key)){
            return -1;
        }
        DLinkedNode* node = cache[key];
        moveToHead(node);
        return node->value;
    }
    
    // 添加元素
    void put(int key, int value) {
        if(!cache.count(key)){
            DLinkedNode* node = new DLinkedNode(key, value);
            cache[key] = node;
            addToHead(node);
            size++;
            if(size > capacity){
                DLinkedNode* removed = removeTail();
                cache.erase(removed->key);
                delete removed;
                size--;
            }
        }else{
            DLinkedNode* node = cache[key];
            node->value = value;
            moveToHead(node);
        }
    }

    // 将节点加入头部
    void addToHead(DLinkedNode* node){
        // 注意这里顺序也不能改变
       node->next = head->next;
       head->next->prev = node;
       head->next = node;
       node->prev = head;
       
    }

    // 将节点移动到头部
    void moveToHead(DLinkedNode* node){
        //顺序不能反
        removeNode(node);
        addToHead(node);
    }

    // 删除节点
    void removeNode(DLinkedNode* node){
        node->next->prev = node->prev;
        node->prev->next = node->next;
    }

    // 删除并返回尾节点
    DLinkedNode* removeTail(){
        DLinkedNode* node = tail->prev;
        removeNode(node);
        return node;
    }
  
};


字符串

strStr函数

image-20230928152313972

思路：

​ strstr() 函数搜索一个字符串在另一个字符串中的第一次出现。

  1. KMP算法，没搞懂过
  2. 遍历，效率低
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int strStr(string haystack, string needle) {
        int size = needle.size();
        int n = haystack.size();
        for(int i = 0; i <= n - size; i++){
            int l = i , r = i + size;
            int index = 0;
            while (l + index < r){
                if(haystack[l + index] != needle[index]){
                    break;
                }
                index++;
            }
            if(index == size){
                return i;
            }
        }
        return -1;
    }
};

子串统计类问题

  • 子串统计类问题的通用技巧：
    • 将所有子串按照其末尾字符的下标分组
    • 考虑两组相邻的子串：以s[i - 1]结尾的子串和以s[i] 结尾的子串
    • 以 s[i] 结尾的子串，可以看成是以 s[i−1] 结尾的子串，在末尾添加上 s[i]组成。

字符串的总引力

image-20231105145220795

思路：

  • 从左往右遍历s，考虑将s[i]添加到以s[i - 1]结尾的子串末尾。添加后，这些以s[i - 1]结尾的子串引力值如何改变
    • 若s[i]之前没有出现过，那么这些子串引力值都会增加1。这些子串的引力值之和会增加i，再加上1，即s[i]单独组成的子串的引力值
    • 若s[i]之前出现过，设最后一次出现的下标为j，那么子串s[0..i - 1] s[1..i -1] …s[j..i- 1]末尾添加s[i]数量不会发生改变。而子串s[j +1..i - 1] .. s[i - 1..i - 1]的引力值会+ 1，即i - j - 1,再 +1，即s[i]单独组成的子串的引力值
  • 上述过程只需要遍历s的过程中用一个变量sumG维护以s[i]结尾的子串的引力值之和，同时用一个数据结构记录上一次出现的下标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    long long appealSum(string s) {
        long long ret = 0;
        vector<int> last_appear(26, -1);
        int sum_index = 0;
        for(int i = 0; i < s.size(); i++){
            int c = s[i] - 'a';
            // 两种情况可以合并成一个表达式,以i为下标时的总引力数
            sum_index += i - last_appear[c];
            ret += sum_index;
            // 更新最后一次出现的下标
            last_appear[c] = i;
        }
        return ret;
    }
};

子数组不同元素的数目平方和

image-20231105151839313

与上题不同是将值变成了平方和

  • 上一题只需要知道加上第i个数之前数的长度是多少，现在需要知道各数之和是多少

  • lazy线段树

区间和

求区间的交集

image-20231003105529539

思路：要求至少射出的数量，其实就是求交集之后有多少互不相关的集合。

每遍历一次，与集合求一次交集：

​ mergerd.back()[0] = max(mergerd.back()[0], left);

​ mergerd.back()[1] = min(mergerd.back()[1], right)；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int n = points.size();
        sort(points.begin(),points.end());
        vector<vector<int>> mereged;
        for(int i = 0; i < n; i++){
            int left = points[i][0];
            int right = points[i][1];
            if(mereged.size() == 0  || mereged.back()[1] < left){
                mereged.push_back({left, right});
            }
            // 注意这里是去交集而不是取并集
            mereged.back()[0] = max(left, mereged.back()[0]);
            mereged.back()[1] = min(right, mereged.back()[1]);
        }
        return mereged.size();
    }
};

image-20231003112134539

思路：

​ 与上题思路一模一样，求交集，算差值，差值即为移除区间的最小数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if (intervals.empty()) {
            return 0;
        }
        vector<vector<int>> mergerd;
        sort(intervals.begin(), intervals.end());
        int n = intervals.size();
        for(int i = 0; i < n; i++){
            int left = intervals[i][0];
            int right = intervals[i][1];
            if(mergerd.size() == 0 || mergerd.back()[1] <= left){
                mergerd.push_back({left,right});
            }
            mergerd.back()[0] = max(mergerd.back()[0], left);
            mergerd.back()[1] = min(mergerd.back()[1], right);
        }
        return n - mergerd.size();
    }
};

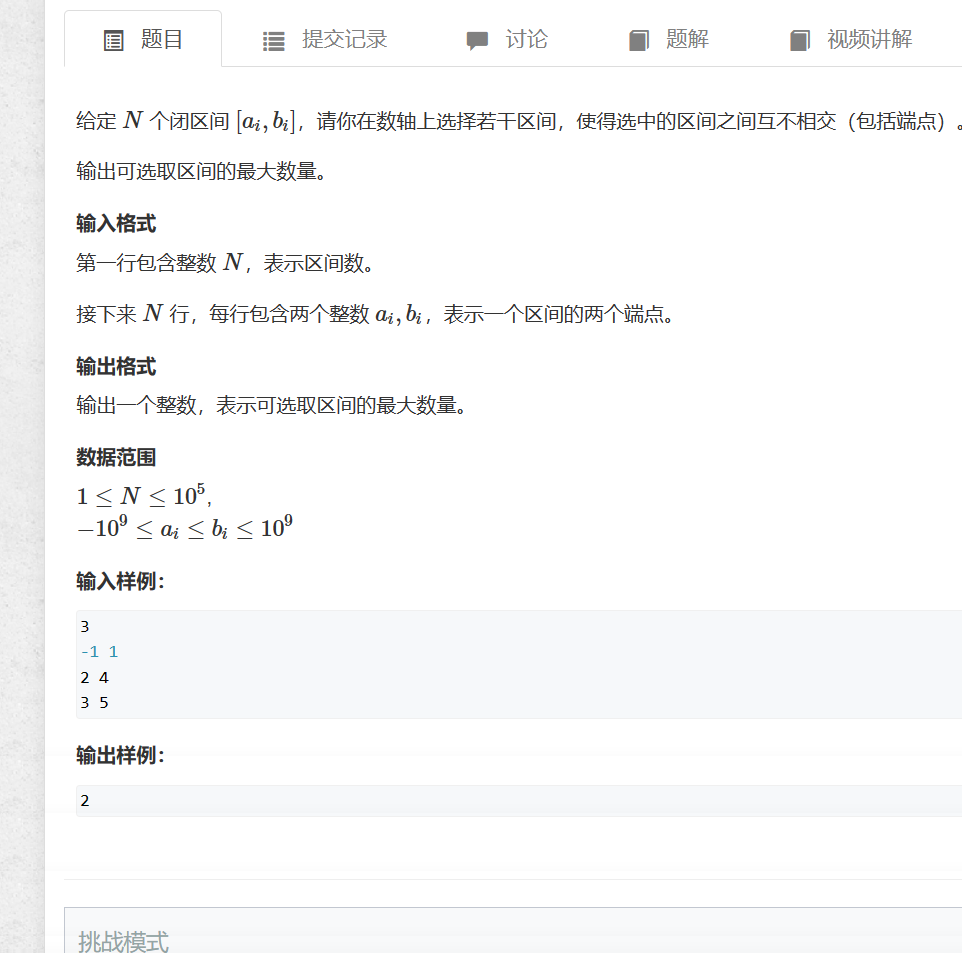
最大不相交区间数量

image-20231102100855691

注意：最大不相交问题，排序时候需要用右端点。如果用左端点存在一个问题：区间长度可以很大，求不出最小值

方法二：同样可以使用求交集的办法。排序默认使用左端点递增

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <algorithm>
#include <vector>


using namespace std;

const int N = 100010;
vector<vector<int>> nums;
int n;

int main(){
    scanf("%d", &n);
    while(n--){
        int l, r;
        scanf("%d %d", &l, &r);
        nums.push_back({l, r});
    }
    
    vector<vector<int>> ret;
    sort(nums.begin(), nums.end(), [](auto a, auto b){
        return a[1] < b[1]; 
    });
    ret.push_back(nums[0]);
    n = nums.size();
    for(int i = 1; i < n; i++){
        if(nums[i][0] > ret.back()[1]){
            ret.push_back(nums[i]);
        }
    }
    cout << ret.size() << endl;
}

排序

快速排序

思路：

​ 基于分治

  • 1.先随便在数组中找一个值作为分界点
    • 直接取左边界，作为x
  • 2.根据x调整区间
    • 所有<x的值在x左边
    • 所有>x的值在x右边
  • 3.递归处理左右两端
  • 做法：
    • 左右lr指针，当左边的数满足小于x时，l++；右边的数大于x时，r–。否则交换两个数。这样遍历一次之后满足l左边的数都小于等于x，r右边的数都大于等于x
  • 期望时间复杂度O(nlogn)
    • 每次层递归需要o(N)
    • 总共有logN层
    • 时间复杂度N*logN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
 #include <iostream>
using namespace std;

const int N = 1e6 + 10;
int q[N];

void quick_sort(int q[], int l , int r){
    if(l >= r){
        return;
    }
    int i = l - 1;
    int j = r + 1;
    int x = q[l + r >> 1];
    while(i < j){
        do{
            i++;
        }while(q[i] < x);
        do{
            j--;
        }while(q[j] > x);
        
        if(i < j){
            swap(q[i], q[j]);
        }
    }
    quick_sort(q, l ,j);
    quick_sort(q, j + 1, r);
}


int main(){
    int n;
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &q[i]);
    }
    quick_sort(q, 0, n - 1);
    for(int i = 0; i < n; i++){
        printf("%d ", q[i]);
    }
    return 0;
}

归并排序

思路

​ 主要思想还是分治，但是具体分法与快速排序不同。

​ 快速排序是先处理在递归，归并排序是先递归在处理

  • 1.确定分界点 mid = (l + r) > 1;

  • 2先递归排序

  • 3.将两个有序的数组合并成一个数组.归并

  • 时间复杂度O(nlogn)

    • 每次层递归需要o(N)
    • 总共有logN层
    • 时间复杂度N*logN
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
 #include <iostream>

using namespace std;

const int N = 100010;
int q[N], tmp[N]; //开辟一个额外数组
int n;


void merge_sort(int q[], int l, int r){
    if(l >= r){
        return;
    }
    int mid = ((r - l) >> 1) + l;
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);
    int i = l, j = mid + 1;
    int k = 0;
    while(i <= mid  && j <= r){
        if(q[i] < q[j]){
            tmp[k++] = q[i++];
        }else{
            tmp[k++] = q[j++];
        }
    }
    while(i <= mid){
         tmp[k++] = q[i++];
    }
    while(j <= r){
         tmp[k++] = q[j++];
    }
    k = 0;
    for(i = l; i <= r;){
        q[i++] = tmp[k++];
    }
}


int main(){
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%d", &q[i]);
    }
    merge_sort(q,0, n - 1);
    for(int i = 0; i < n; i++){
        printf("%d ", q[i]);
    }
}

堆排序

堆是一颗二叉树(完全二叉树 除了最后一层外，所有节点都是非空的)

  • 小根堆：每个节点≤左右儿子

    • 根节点是最小值

  • 存储方式

    • 堆用一个一维数组存储，注意下标从1开始
    • 1号节点为根节点。
    • x的左儿子：2x
    • x的右儿子：2x+ 1

  • STL优先队列中的底层是堆

  • 两个基本操作

    • down(x)
      • 将一个大的数往下走
    • up(x)
      • 将一个小的数往上走

  • 其他操作可以由这两个基本操作得出

    • 插入：在整个堆的最后一个元素后加入x，up
    • 最小值：整个数组的第一个元素
    • 删除最小值：用整个堆(数组)的最后一个元素覆盖第一个元素，再down
    • 删除任意一个元素k：用最后一个元素覆盖掉heap[k]。再做一次down和up操作
    • 修改任意一个元素k heap[k] = x,再做一次down和up
  • 堆排序：递增排序
    • 每次找出最小值，再删除最小值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 100010;
int n, m;
int heap[N];

void down(int u){
    int t = u;
    // 判断当前根节点是否是最小值,若不是则交换
    if(u * 2 <= n && heap[u * 2] < heap[t]){
        t = u * 2;
    }
    if(u * 2 + 1 <= n && heap[u * 2 + 1] < heap[t]){
        t = u * 2 + 1;
    }
    if(t != u){
        swap(heap[t], heap[u]);
        // 递归遍历
        down(t);
    }
}


int main(){
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++){
        scanf("%d", &heap[i]);
    }
    // 时间复杂度O(N)
    for(int i = n /2; i >= 0; i--){
        down(i);
    }
    while(m--){
        cout << heap[1] << " ";
        // 删除最小值
        heap[1] = heap[n];
        n--;
        down(1);
    }
}

拓扑排序

  • 入度为0的边都可以作为起点，所以用一个队列维护入度为0的节点
  • 宽度搜索，每次取出队头t，枚举t的所有出边 ，枚举其边t->j，减少j的入度
    • 若j的入度为0，加入队列
  • 用数组模拟队列的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <cstring>

using namespace std;
const int N = 100010;

// 邻接表的表示
int h[N], ne[N], e[N], idx;
// 记录出度和入度
int d[N],q[N];
int n, m;

bool topsort(){
    int hh = 0, tt = -1;
    for(int i = 1; i <= n; i++){
        if(d[i] == 0){
            // 入度为0, 加入队列
            q[++tt] = i;
        }
    }
    while(hh <= tt){
        int t = q[hh++];
        for(int i = h[t]; i != -1; i = ne[i]){
            int j = e[i];
            d[j]--;
            if(d[j] == 0){
                q[++tt] = j;
            }
        }
    }
    return tt == n - 1;
}

// a->b
void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

int main(){
    memset(h, -1, sizeof(h));
    scanf("%d%d", &n,&m);
    while(m--){
        int a, b;
        scanf("%d%d", &a,&b);
        add(a,b);
        d[b]++;
    }
    if(topsort()){
        for(int i = 0; i < n; i++){
            printf("%d ", q[i]);
        }
        puts("");
    }else{
        puts("-1");
    }
}

链表

k个一组翻转链表

image-20231011130338252

思路：

​ 需要用三个指针在k个数内反转：pre，start和next，这里逻辑简单来说就是将start链表的下一个元素指向pre，具体逻辑不在赘述

​ 需要注意的是到第k个数如何解决：cur指针记录的是上k个数的最后一个数，所以tail尾指针应该是cur->next，也就是反转前当前k个数的第一个数，反转后的最后一个数。它的下一个元素指向下一组的第一个元素，即为现在的start。前k个数的最后一个数(pre)现在变为首元素。让cur->next 指向当前分组的头结点，再将cur更新为当前分组的尾结点。做到上一个分组的尾结点与当前分组的头结点相连接。最后再更新链表长度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
*/
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        // 创建一个虚拟头节点，方便处理头部的情况
        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        int len = 0; // 链表长度计数
        ListNode* cur = dummy;
        
        // 计算链表长度
        while (cur->next) {
            len++;
            cur = cur->next;
        }
        
        cur = dummy;
        
        // 当链表长度大于等于 K 时，执行翻转操作
        while (len >= k) {
            ListNode* pre = nullptr;
            ListNode* next = nullptr;
            ListNode* start = cur->next;
            
            // 翻转 K 个节点
            for (int i = 0; i < k; i++) {
                next = start->next;
                start->next = pre;
                pre = start;
                start = next;
            }
            
            ListNode* tail = cur->next; // 当前分组的尾节点
            cur->next = pre; // 当前分组的头节点
            tail->next = start; // 当前分组的尾节点指向下一组的头节点
            cur = tail; // 更新当前节点为尾节点
            len -= k; // 更新剩余链表长度
        }
        
        return dummy->next;
    }
};

合并k个有序链表

image-20231115151008669

  • 思路
  • 将k个链表看成k次两个链表的合并
  • 这样问题就变成了双链表合并
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* a, ListNode* b){
        if(!a || !b){
            return a == nullptr ? b : a;
        }
        ListNode* head = new ListNode();
        ListNode* tail = head;
        ListNode* aPtr = a, *bPtr = b;
        while(aPtr && bPtr){
            if(aPtr->val < bPtr->val){
                tail->next = aPtr;
                aPtr = aPtr->next;
            }else{
                tail->next = bPtr;
                bPtr = bPtr->next;
            }
            tail = tail->next;
        }
        tail->next = (aPtr == nullptr) ? bPtr : aPtr;
        return head->next;
    }

    ListNode* merge(vector<ListNode*> lists, int l, int r){
        if(l == r){
            return lists[l];
        }
        if(l > r){
            return nullptr;
        }
        int mid = l + ((r - l) >> 1);
        return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
    }
    
    ListNode* mergeKLists(vector<ListNode*>& lists) {
       return merge(lists, 0, lists.size() - 1);
    }
};

环形链表

image-20231115153336756

  • 思路
    • 快慢指针，两指针相遇即有环
    • 怎么找到入口：
      • image-20231115154718554
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast){
                slow = head;
                while(slow != fast){
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }

        return nullptr;
    }
};

滑动窗口

最短且字典序最小的美丽子字符串

image-20231016093534315

思路：

​ 最开始枚举长度为k的子字符串，一次递增到字符串长度。

​ 寻找字典序最小的子字符串，更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    string shortestBeautifulSubstring(string s, int k) {
        if(count(s.begin(), s.end(), '1') < k){
            return "";
        }
        for(int size = k;;size++){
            string ans = "";
            // i表示起点
            for(int i = size; i <= s.size(); i++){
                string t = s.substr(i - size, size);
                if((ans =="" || t < ans) && count(t.begin(), t.end(), '1') == k){
                    ans = t;
                }
            }
            if(!ans.empty()){
                return ans;
            }
        }
        return "";
    }
};
文章作者: jingxiaoyang
文章链接: https://yangjx29.github.io/posts/b7e144d1.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 jingxiaoyang !
无标签
赏
评论
  目录